Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T17:57:13.786Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Calculation of the Generalised Poisson Function

Published online by Cambridge University Press:  29 August 2014

Erkki Pesonen
Erkki Pesonen*
Affiliation:
Helsinki
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Drs. H. Bohman and F. Esscher have reported in a recent paper) an extensive research performed in Sweden on the different methods of calculation of the distribution function of the total amount of claims. In the present paper certain methods are discussed in so far as they are different from those presented in the above quoted paper. The consideration is restricted to the generalised Poisson function even though some results can be easily extended. The author has already commented on some of the results represented in the sequel at a special meeting of the 17th International Congress of Actuaries in Edinburgh.

I. Lemma. Let 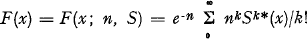be the generalised Poisson function under investigation. If 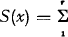aiSi(x), where Σ ai = 1 (the functions Si need not be distribution functions, neither must the constants ai be real numbers of interval [0,1]), then

F(x; n, S) = F(.; a1n, S1) * …*F(.; arn, Sr) (x),

as is easily verified by the use of characteristic functions. This component representation is repeatedly used in the sequel.

2. A Modified Esscher Method. The Esscher method is based on an observation that the well-known Edgeworth expansion is more advantageously applicable to a conveniently modified distribution function instead of the original generalised Poisson function. Let us assume that the value of F(x) is required at a point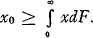

Type
Astin Colloquium 1965 Lucerne Subject one
Information
ASTIN Bulletin: The Journal of the IAA , Volume 4 , Issue 2 , February 1967 , pp. 120 - 128
Copyright
Copyright © International Actuarial Association 1967

References

page 120 note 1) Bohman, H. and Esscher, F.: Studies in Risk Theory with Numerical illustrations Concerning Distribution Functions and Stop Loss Premiums. Part I.—Skandin. Aktuarietidskrift, 3-4 (1963), pp. 172–225Google Scholar.

page 126 note 1) Let Then so that if ν = n(S(ξ) – S(tξ)), then the necessary condition for normal approximation gives a rule ν ≥t —6/72πε2. In a sense an optimal value of t is reached by requiring that the needed mean number of claims to length unit, ξ1 as a measure, reaches its minimum. By differentiating the result t = 5/6; is obtained.