Let F(x) be the distribution function of the total amount ξ of claims of an insurance company. It is assumed that this company reduces its liability by means of one or several reinsurance arrangements. Let the remaining part of claims amount be equal to η, which is another random variable. Reinsurance arrangements are supposed to fulfil the following consistency condition: if ξ = x, then almost certainly o ≤ η ≤ x. Presumably all reinsurance arrangements occuring in practice can be supposed to fulfil this requirement.

The problem is to find an optimal reinsurance arrangement, i.e. an optimal random variable η, in the sense that, the net reinsurance premium being given, the variance of η reaches its minimum. In other words, a variable η is looked for, which gives

E{η} = P = const.; V{η} = minimum

In the sequel we use conditional expectations in the sense defined by DOOB ([I]).

Let η be an arbitrary random variable satisfying the consistency condition. If

R(x) = E{η|ξ =x},

then evidently ≤ R(x) ≤ x. Further we have

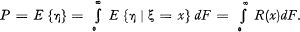
For the variance the inequality

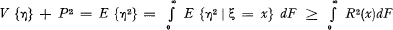
holds true, since

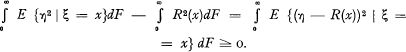
Clearly the arrangement E {η|ξ} gives also to the reinsurer a smaller variance than the original arrangement.