Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T14:49:47.721Z Has data issue: false hasContentIssue false
  • English
  • Français

On Esscher Transforms in Discrete Finance Models

Published online by Cambridge University Press:  29 August 2014

Hans Bühlmann ,
Freddy Delbaen ,
Paul Embrechts  and
Albert N. Shiryaev
Hans Bühlmann*
Affiliation:
Department of Mathematics, ETH Zürich
Freddy Delbaen*
Affiliation:
Department of Mathematics, ETH Zürich
Paul Embrechts*
Affiliation:
Department of Mathematics, ETH Zürich
Albert N. Shiryaev*
Affiliation:
Steklov Mathematical Institute, Moscow
*
Department of Mathematics, ETH Zürich, CH – 8092 Zürich, Switzerland
Department of Mathematics, ETH Zürich, CH – 8092 Zürich, Switzerland
Department of Mathematics, ETH Zürich, CH – 8092 Zürich, Switzerland
Steklov Mathematical Institute, Ulitza Vavilova 42, Moscow 117966, GSP-1, Russia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The object of our study is

where each Sn is a m-dimensional stochastic (real valued) vector, i.e.

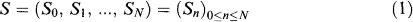
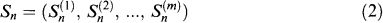
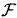denned on a probability space (Ω, , P) and adapted to a filtration (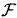n)0≤n≤N with 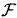0 being the σ-algebra consisting of all null sets and their complements. In this paper we interpret 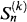as the value of some financial asset k at time n.

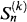Remark: If the asset generates dividends or coupon payments, think of as to include these payments (cum dividend process). Think of dividends as being reinvested immediately at the ex-dividend price.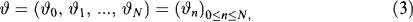

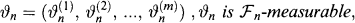
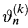Definition 1

(a) A sequence of random vectors

where

is called a trading strategy. Since our time horizon ends at time N we must always have ϑN ≡ 0.

The interpretation is obvious: stands for the number of shares of asset k you hold in the time interval [n,n + 1). You must choose ϑn at time n.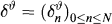

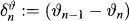(b) The sequence of random variables

where Sn stands for the payment stream generated by ϑ (set ϑ−1 ≡ 0).

Type
Articles
Information
ASTIN Bulletin: The Journal of the IAA , Volume 28 , Issue 2 , November 1998 , pp. 171 - 186
Copyright
Copyright © International Actuarial Association 1998

References

[1]Borch, K. (1962). Equilibrium in a reinsurance market. Econometrica 30, 424–444.CrossRefGoogle Scholar
[2]Bühlmann, H. (1984). The general economic premium principle. ASTIN Bulletin 14, 13–21.CrossRefGoogle Scholar
[3]Duffie, D. (1996). Dynamic Asset Pricing Theory, 2nd edition, Princeton University Press.Google Scholar
[4]Gerber, H.U. and Shiu, Elias S.W. (1994). Option pricing by Esscher transforms. Transactions of the Society of Actuaries, vol. XLVI, pp. 99–140.Google Scholar
[5]Rogers, L.C.G. (1994). Equivalent martingale measures and no-arbitrage. Stochastics and Stochastics Reports 51, 41–49.CrossRefGoogle Scholar
[6]Rogers, L.C.G. (1997). The potential approach to the term structure of interest rates and their foreign exchange rates. Mathematical Finance 7, 157–176.CrossRefGoogle Scholar
[7]Schachermayer, W. (1992). A Hilbert space proof of the fundamental theorem of asset pricing in finite discrete time. Insurance: Mathematics and Economics 11, 249–257.Google Scholar