Published online by Cambridge University Press: 29 August 2014
It is likely that in the future applications of actuarial methods to the decision making in non-life companies will more and more relate to the utility concept as was proposed by K. Borch [1] about fifteen years ago. In this connection it will be important to have workable numerical methods. The calculation of the distribution function of the profit is an unavoidable problem from a practical point of view. Even if it is possible to compute this function today accurately with computers by using the ingenious technique developed by H. Bohman [2], integrals become very laborious when applied to the decision making procedure based on utility concepts. This paper intends to show that the NP-technique,—proposed for the first time by L. Kauppi and P. Ojantakanen in actuarial science [3]—, is particularly suitable in integrals needed for utility calculations.
LetF(x) be the distribution function of the total amount of claims and let its mean, standard deviation, skewness and kurtosis be respectively m, σ, γ1 and γ2. The NP-technique uses the system of equations
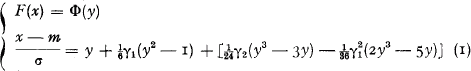
where Φ(y) is the standardized normal distribution function. If the parameters m, σ, γ1 and γ2 and F(x) are known, y is directly found from the tables of the normal distribution function, and thereafter the second equation directly gives the value of x. If, vice versa, x and the above parameters are known, F(x) is obtained by solving y from the second equation (1), or, more practically, by using the converted NP-expansion instead of (i), i.e. [4]:
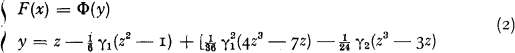
where 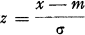
Sometimes it is sufficient to use short forms of the formulae (1) and (2), obtained by omitting the terms in the brackets. If these rougher approximations are used, the estimation of the kurtosis γ2 remains unnecessary.