Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T13:28:40.408Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on the Background to the Subject: Theory of Risk, Fundamental Mathematics and Applications

Published online by Cambridge University Press:  29 August 2014

Carl Philipson
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

By a general theorem the necessary and sufficient condition for a function φ0 (σ) being completely monotonic for σ lying in the right semi-plane, i.e. that the nth derivative with respect to σ has the sign of (— 1)n, is that the function may be represented by the Laplace-Stieltjes integral 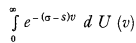, where U (v) is a non-decreasing function of v, independent of σ and bounded in every finite interval, σ a real or complex variable represented in the right semi-plane, s a real constant ≤ the real part of σ. By the notation φn (σ) we designate 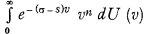, which for U (v) being independent of σ, as assumed above, is equal to .

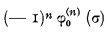Definition 1. A compound Poisson process (in the narrow sense) is a process for which the probability distribution of the number of changes in the random function Y (t), constituting the process, occurring while the parameter, which is represented on the positive real axis, is in the interval (o, t) for every value of t, is defined by the following relation

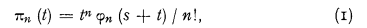
the function φn (σ) being defined by the integral given above and subject to the condition that φ0 (σ) tends to unity, when σ tends to s. The function U (v) in the integrand of φn (σ) is, then, a distribution function which defines the risk distribution, in this case said to be t-independent.

Type
Research Article
Information
ASTIN Bulletin: The Journal of the IAA , Volume 1 , Issue 5 , July 1961 , pp. 256 - 264
Copyright
Copyright © International Actuarial Association 1961

References

Literature Cited

Almer, B., 1957: “Risk Analysis in Theory and Practical Statistics”, Trans, XV.Google Scholar
Ammeter, H., 1946: “Das Maximum des Selbstbehaltes in der Lebensversicherung unter Berücksichtigung der Rückversicherungskosten”, Bas, 48.Google Scholar
Ammeter, H., 1948: “A Generalization of The Collective Theory of Risk in regard to Fluctuating Basic Probabilities,” SA.Google Scholar
Ammeter, H., 1949: “Die Elemente der Kollektiven Risikotheorie von festen und zufallsartig schwankenden Grundwahrscheinlichkeiten”, Bas, 49.Google Scholar
Ammeter, H., 1951: “The Calculation of Premium Rates for Excess of Loss and Stop Loss Reinsurance Treaties”, Trans, XIII.Google Scholar
Ammeter, H., 1954: “Risikotheoretische Methoden der Rückversicherung”, Trans, XIV.Google Scholar
Ammeter, H., 1955: “La théorie du risque et l'assurance des choses”, Bas, 54.Google Scholar
Ammeter, H., 1957a: “Anwendungen der kollektiven Risikotheorie auf Probleme der Risikopolitik in Sachversicherungen”, Trans, XV.Google Scholar
Ammeter, H., 1957b: “A Rational Experience Rating Technique for Group Insurance on the Risk Premium Basis”, Trans, XV.Google Scholar
Ammeter, H., 1957c: “Die Ermittlung der Risikogewinne in Versicherungswesen auf risikotheoretischer Grundlage”, Bas, 57.Google Scholar
Ammeter, H., 1960: “Stop Loss Cover and Experience Rating”, Trans, XVI.Google Scholar
Arfwedson, G., 1955: “Research in Collective Risk Theory”, SA.Google Scholar
Bailey, W. N., 1935: “Generalized Hypergeometric Series”, CMT, 32.Google Scholar
Bartlett, M. S., 1954: “Processus stochastiques ponctuels”, AIP, XIVGoogle Scholar
Bartlett, M. S., 1959: “The Impact of Stochastic Process Theory on Statistics”, HCV.Google Scholar
Benktander, G., Segerdahl, C. O., 1960: “On the Analytical Representation of Claim Distributions with special Reference to Excess of Loss Reinsurance, Trans, XVI.Google Scholar
Bichsel, F., 1959: “Une méthode pour calculer une ristourne adéquate pour années sans sinistres, AB, I, 3.Google Scholar
Cramér, H., 1919: “Bidrag till utjämningsförsäkringens teori”, Stockholm (Försäkringsinspekt.), 1919.Google Scholar
Cramér, H., 1926: “A Review of F. Lundberg”, SA.Google Scholar
Cramér, H., 1928: “On the Composition of Elementary Errors”, SA.Google Scholar
Cramér, H., 1930: “On the Mathematical Theory of Risk”, Stockholm, Skandia Jubilee Volume, 1930.Google Scholar
Cramér, H., 1946: Mathematical Methods of Statistics, Princeton, Math. Series.Google Scholar
Cramér, H., 1954: “On Some Questions connected with the Mathematical Risk”, UCP, 2.Google Scholar
Cramér, H., 1955: “Collective Risk Theory, A Survey from the Point of View of the Theory of Stochastic Processes”, Stockholm, Skandia Jubilee Volume, 1955.Google Scholar
Delaporte, P., 1959: Quelques problèmes de statistique mathématique posés par l'assurance automobile et le bonus pour non sinistre” Baf, 65.Google Scholar
Delaporte, P., 1960: “Un problème de tarification de l'assurance accidents d'automobiles examiné par la statistique mathématique”, Trans, XVI.Google Scholar
Depoid, P., 1959: “Etud e de la fréquence et de la bonification pour non sinistre dans un portefeuille ‘tous risques modernes’“, Baf, 65.Google Scholar
Esscher, F., 1932: “On the Probability Function in the Collective Theory of Risk”, SA.Google Scholar
Feller, W., 1943: “On a General Class of ‘Contagious’ Distributions”, AMS, 14.Google Scholar
Feller, W., 1950: Probability Theory and Its Applications, Vol. I, 1st ed., New York 1950.Google Scholar
Feller, W., 1957: Probability Theory and Its Applications, Vol. I, 2nd ed., New York 1957.Google Scholar
Franckx, Ed., 1959: “Théorie de bonus. Consequences de l'étude de M. le Professeur Fréchet”, AB, I, 3.Google Scholar
Franckx, Ed., 1960: Stencil read to the Astin meeting, Brussels.Google Scholar
Fréchet, M., 1959: “Essai d'une étude des successions de sinistres considérés comme processus stochastique”, Baf, 65.Google Scholar
Grenander, U., 1957: “Some Remarks on Bonus Systems in Automobile Insurance”, SA.Google Scholar
Hofmann, M., 1955: “Über zusammengesetzte Poisson-Prozesse und ihre Anwendungen in der Unfallsversicherung”, Bas, 55.Google Scholar
Lévy, P., 1937: Théorie de l'addition des variables aléatoires, Paris, 1937.Google Scholar
Lundberg, Filip, 1903: Approximerad framställning av sannolikhetsfunktionen, Återförsäkring av kollektivrisker, Akad. Afhandl., Uppsala, 1903.Google Scholar
Lundberg, Filip, 1909: “Zur Theorie der Rückversicherung”, Trans, Wien.Google Scholar
Lundberg, Filip, 1919: “Teorin för riskmassor”, Stockholm (Försäkringsinspekt.) 1919.Google Scholar
Lundberg, Filip, 1926–1928: Försäkringsteknisk utjämning, Stockholm, 1926–1928.Google Scholar
Lundberg, Filip, 1930: “Über die Wahrscheinlichkeitsfunktion einer Risikenmasse”, SA.Google Scholar
Lundberg, Filip, 1932: “Some Supplementary Researches on the Collective Risk Theory”, SA.Google Scholar
Lundberg, Filip, 1934: “On the Numerical Application of the Collective Risk Theory”, Stockholm, De Förenade Jubilee Volume, 1934.Google Scholar
Lundberg, Ove, 1940: On Random Processes and Their Application to Sickness and Accident Statistics, Inaugural Dissertation, Uppsala, 1940.Google Scholar
Matérn, B., 1960: “Spatial Variation, Stochastic Models and Their Application to some Problems in Forest Surveys and other Sampling Investigations”, Inaugural Dissertation, BFR, 49.Google Scholar
Mehring, J., 1960: “Strukturprobleme der Kraftfahrt-Haftpflichtversicherung”, BDGV.Google Scholar
Odhnoff, W., 1946: “Some studies of the Characteristic Functions and the Semi-Invariants of Pearson's Frequency-Functions, ASFL.Google Scholar
Philipson, C., 1955: “A Tentative Application of The Collective Risk Theory to Crop Insurance”, SA.Google Scholar
Philipson, C., 1956: “A Note on Different Models of Stochastic Processes dealt with in the Collective Theory of Risk, SA.Google Scholar
Philipson, C., 1957: “Some Distribution Functions related to a Specified Class of Stochastic Processes, Trans, XV.Google Scholar
Philipson, C., 1959a: “A Contribution to the Problem of Estimation involved in an Insurance against Loss of Profit”, SA.Google Scholar
Philipson, C., 1959b: “A Method for the Estimation of the Risk Premiums in Stop Loss Reinsurance, AB, I, 2.Google Scholar
Philipson, C., 1960: “A General Survey of Problems involved in Motor Insurance” (to be published), Trans, XVI.Google Scholar
Philipson, C., 1961a: “Note on the Application of Compound Poisson Processes to Sickness and Accident Statistics”, AB, I, 4.Google Scholar
Philipson, C., 1961b: “The Theory of Confluent Hypergeometric Functions and Its Application to Compound Poisson Processes” (to be published), SA.Google Scholar
Philipson, C., 1961c: “On a Class of Distribution Functions as applied to Different Stochastic Processes” (to be published), SA.Google Scholar
Quenouille, M., 1949: “Problems in Plane Sampling”, AMS, 20.Google Scholar
Sparre Andersen, E., 1957: “On the Collective Theory of Risk in the case of Contagion between the Claims”, Trans, XVI.Google Scholar
Segerdahl, C. O., 1959: “A Survey of Results in the Collective Theory of Risk”, HCV.Google Scholar
Slater, L. J., 1960: Confluent Hypergeometric Functions, Cambr. Univ. Press.Google Scholar
Thompson, H., 1954: “A Note on Contagious Distributions”, B, XLI.Google Scholar
Thompson, H., 1955: “Spatial Point Processes with Application to Ecology”, B, XLII.Google Scholar
Thyrion, P., 1959: “Contribution à l'étude de bonus pour non sinistre en assurance automobile”, AB, I, 3.Google Scholar
Thyrion, P., 1960: “Étude de la loi de probabilité de la variable “nombre de sinistres” dans l'assurance automobile”, Trans, XVI.Google Scholar
Wilhelmsen, L., 1955: “Den kollektive riskteoris anvendelse i skadeforsikring” (stencil), NTA.Google Scholar