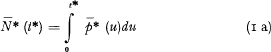In order to fix our ideas an illustration of the theory for (a) a general elementary random process, (b) a compound Poisson process and (c) a Polya process shall be given here below following Ove Lundberg (On Random Processes and Their Application to Accident and Sickness Statistics, Inaug. Diss., Uppsala 1940).

Let the continuous parameter t* be measured on an absolute scale from a given point of zero and consider the random function N* (t*) which takes only non-negative and integer values with N* (o) = o. This function constitutes a general elementary random process for which the conditional probability that N* (t*) = n relative to the hypothesis that 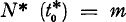shall be denoted 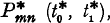, while the absolute probability that N* (t) = n i.e. 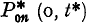shall be written 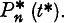If quantities of lower order than dt* are neglected, we may write 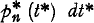for the conditional probability that N* (t* + dt*) = n + 1 relative to thehyp othesis that N* (t*) = n, i.e. 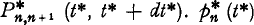is the intensity function of the process which is assumed to be a continuous function of t* (the condition of existence for the integral over the given interval of t* for every n > m may be substituted for the condition of continuity). The expectations for an arbitrary but fix value of t* of N* (t*) and p* (t*) will be denoted by the corresponding symbol with a bar so that

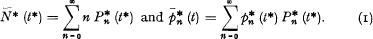
If 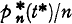is uniformly bounded for all n in the interval o ≤ t* < T*, where T* is an arbitrary but fix value of t*, we have i.a. that