In the past the subject of optimal reinsurance has been dealt with by various authors such as Borch (1), Kahn (2) and Verbeek (3). Borch tries to look at the problem from the point of view of a company which acts as both Insurer and Reinsurer whereas the viewpoint of Kahn and Verbeek is that of a Ceding Company.

Let us study the simplest possible market situation of one Insurance Company C and one Reinsurer R. C writes a portfolio P and seeks reinsurance protection at R.

In the present note I will start with the viewpoint of optimizing simultaneously the situation of C and R.

For both C and R the variance is used as a measure of risk. The variance of P is V. C makes an effort to reduce V to a level Vc by way of a reinsurance treaty T. The corresponding variance of R is VR.

Out of the set of possible reinsurance treaty arrangements {T} we assume that the parties are first of all interested in such arrangements for which

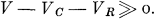
In other words they will look for solutions which will lead to a substantial reduction of the variance.

It is possible to think of “nonsense” arrangements where no substantial reduction is achieved and in the extreme case even of arrangements for which

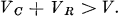
In a further paper we might deal with such a case.