Consider a claim size distribution with complementary d.f. H(.). Let E(x) denote the average claim payment under a policy subject to this claim size d.f. but with a deductible of x. That is

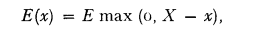
where E is the expectation operator and X is the random variable claim size before application of the excess.

It is well-known—see Benktander and Segerdahl (1960, p. 630)—that:

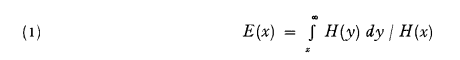
It was shown by them that E(x) is a constant for all x ≥ o if and only if the claim size d.f. is negative exponential:

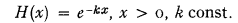
This property of the negative exponential distribution is closely related to the fact that it is the only distribution with constant failure rate. See Kaufmann (1969, pp. 20-22).

The constancy of average excess claim size with varying deductible can be useful in practice. For example, if the distribution of motor vehicle (property damage) claim sizes can be assumed roughly exponential, which will often be reasonable, then a variation in the deductible will not induce any variation in the average size of claims paid by the insurer, i.e. after application of the deductible. This will be a particularly useful piece of information if for example one is examining trends in average claim size over a period during which a change in deductible occurred.