Published online by Cambridge University Press: 29 August 2014
Much of the risk theory literature deals with the total claims distribution 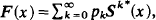 where pk = the probability of k claims and S(x) is the distribution function of severity. Both pk and S(x) are univariate probability distributions. Thus, F(x) can be interpreted as a model of claims from one class of policies or as an aggregate model where pk and S(x) represent mixed probability distributions from a heterogeneous portfolio of policies. An alternative approach to modelling total claims in the latter case would be to recognize explicitly that total claims are the result of the interaction of multivariate processes. In the most general case, total claims arise from a multivariate accident process where each accident triggers multivariate claims frequency and severity processes.
where pk = the probability of k claims and S(x) is the distribution function of severity. Both pk and S(x) are univariate probability distributions. Thus, F(x) can be interpreted as a model of claims from one class of policies or as an aggregate model where pk and S(x) represent mixed probability distributions from a heterogeneous portfolio of policies. An alternative approach to modelling total claims in the latter case would be to recognize explicitly that total claims are the result of the interaction of multivariate processes. In the most general case, total claims arise from a multivariate accident process where each accident triggers multivariate claims frequency and severity processes.
The purpose of this article is to present a multivariate model of total claims and to develop the cumulant generating function of this distribution. Such a model is superior to the traditional model in two respects: (1) It permits explicit recognition of shifts in the overall portfolio composition. Applications of the traditional model, in contrast, rely on the assumption that the portfolio composition is relatively constant over time. (2) It facilitates the evaluation of the effects of reinsurance on the total claims distribution when the reinsurance arrangements are not the same in different segments of the portfolio.