Let us denote by E(x) the pure risk premium of an unlimited excess cover with the retention x and by H(x) and m(x) the corresponding expected frequency and severity.

We thus have E(x) = H(x) · m(x).

H(x) is a non-increasing function of x and for practical purposes we can assume that it is decreasing; H′(x) < o. The equation H(x) = n has then only one solution xn, where n is a fixed integer.

Let En denote the risk premium for a reinsurance covering the n largest claims from the bottom.

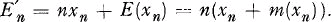Let us define Intuitively we feel that 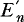is a good approximation for En.

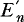We shall first show that when the claims size distribution is Pareto and the number of claims is Poisson distributed, is a good approximation for En, being slightly on the safe side. We further include a proof given by G. Ottaviani that the inequality 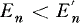always holds.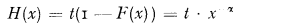

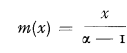In the Pareto case we have

where the Poisson parameter t stands for the expected number of claims in excess of 1 (equal to a suitably chosen monetary unit) and

.