Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-24T01:43:13.986Z Has data issue: false hasContentIssue false
  • English
  • Français

Integration of the normal power approximation

Published online by Cambridge University Press:  29 August 2014

Gottfried Berger
Gottfried Berger*
Affiliation:
Stamford, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the set of functions

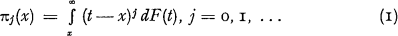
Obviously, π1(x) represents the net premium of the excess cover over the priority x, and 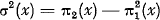the variance thereof.

If a distribution function F(x) = 1 − π0(x) is given, the set (1) can be generated by means of the recursion formulae

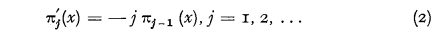
Let us study the special class of d.fs. F(x) which satisfy

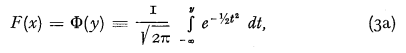
where

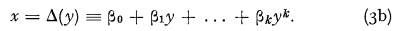
If these conditions are met, the integrals (1) have the solution:

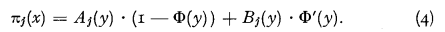
Aj(y) and Bj(y), respectively, are polynomials of rank jk and jk − 1. Their coefficients are determined by the equations:

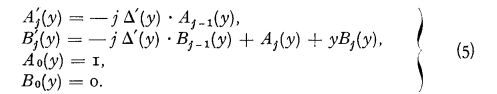
The system (5) is obtained by differentiation of (4) with respect to y, and observing (2).

Type
Research Article
Information
ASTIN Bulletin: The Journal of the IAA , Volume 7 , Issue 1 , December 1972 , pp. 90 - 95
Copyright
Copyright © International Actuarial Association 1972

References

[1]Kauppi, Ojantakanen (1969): “Approximations of the generalized Poisson function”; Astin Bulletin.Google Scholar
[2]Beard. Pentikaeinen, Pesonen (1969): “Risk Theory”; Methuen, London.Google Scholar
[3]Ammeter, (1955). “The calculation of premium rates for excess of loss and stop loss reassurance treaties”; Arithbel, Brussels.Google Scholar
[4]Bohman, Escher (1964): “Studies in Risk Theory…”; Skand. Aktu. Tidskr.Google Scholar
[5]Seal (1971): “Numerical calculation of the Bohman-Escher family convolution-mixed negative binomial distribution functions”; MVSM.Google Scholar