Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T15:24:45.706Z Has data issue: false hasContentIssue false
  • English
  • Français

From Aggregate Claims Distribution to Probability of Ruin

Published online by Cambridge University Press:  29 August 2014

Hilary L. Seal
Hilary L. Seal*
Affiliation:
Ecole Polytechnique Fédérale de Lausanne
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

When the distribution of the number of claims in an interval of time of length t is mixed Poisson and the moments of the independent distribution of individual claim amounts are known, the moments of the distribution of aggregate claims through epoch t can be calculated (O. Lundberg, 1940, ch. VI). Several approximations to the corresponding distribution function, F(·, t), are available (see, e.g., Seal, 1969, ch. 2) and, in particular, a simple gamma (Pearson Type III) based on the first three moments has proved definitely superior to the widely accepted “Normal Power” approximation (Seal, 1976). Briefly,

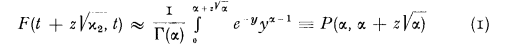
where the P-notation for the incomplete gamma ratio is now standard and α, a function of t, is to be found from

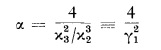
the kappas being the cumulants of F(·, t). An excellent table of the incomplete gamma ratio is that of Khamis (1965).

The problem that is solved in this paper is the production of an approximation to U(w, t), the probability of non-ruin in an interval of time of length t, by using the above mentioned gamma approximation to F(·, t).

Type
Research Article
Information
ASTIN Bulletin: The Journal of the IAA , Volume 10 , Issue 1 , May 1978 , pp. 47 - 53
Copyright
Copyright © International Actuarial Association 1978

References

Cannella, S., 1963. “Variation de la prime d'assurance de l'assistance pharmaceutiquc en fonction de la participation de l'assuré au coût de l'assistance”. ASTIN. Bull. 2, 30–44.CrossRefGoogle Scholar
Hadwiger, H., 1942. “Wahl einer Näherungsfunktion für Verteilungen auf Grund einer Funktionalgleichung”. Bl. Versich. Math. 5, 345–352.Google Scholar
Johnson, N. L., and Kotz, S., 1970. Distributions in Statistics. Continuous Univariate Distributions—1. Houghton Mifflin, Boston.Google Scholar
Khamis, S. H. and Rudert, W., 1965. Tables of the Incomplete Gamma Function Ratio. Von Liebig, Darmstadt.Google Scholar
Lundberg, O., 1940. On Random Processes and their Application to Sickness and Accident Statistics. Almqvist and Wiksell, Uppsala.Google Scholar
Seal, H. L., 1969. Stochastic Theory of a Risk Business. John Wiley, New York.Google Scholar
Seal, H. L. 1974. “The numerical calculation of U(w, t), the probability of non-ruin in an interval (o, t)”. Scand Actu. J. 1974, 121–139.CrossRefGoogle Scholar
Seal, H. L. 1976. “Approximations to Risk Theory's F(x, t) by means of the gamma distribution”. ASTIN Bull. 9, 213–218.CrossRefGoogle Scholar
Shuster, J., 1968. “On the inverse Gaussian distribution function”. J. Amer. Statist. Assn. 63, 1514–1516.CrossRefGoogle Scholar
Tweedie, M. C. K., 1957. “Statistical properties of inverse Gaussian distributions”. Ann. Math. Statist. 28, 362–377 and 696–705.CrossRefGoogle Scholar