The Esscher premium principle has recently had some exposure, namely, with the works of Bühlmann (1980) and Gerber (1980).

Bühlmann (1980) devised the principle and coined the name for it within the framework of utility theory and risk exchange. Geruber (1980), on the other hand, gives further insight into the principle by studying it within the realm of forecasting in much the same spirit as credibility theorists forecast premiums. However, there is an important distinction: the choice of loss function.

The present note sets out to criticize this relatively embryonic principle using decision theoretic arguments and indicates that the Esscher premium is essentially a small perturbation of the well established linearized credibility premium Bühlmann (1970).

Let H denote the Esscher premium principle with loading h > o. That is, if X is an observable random variable and Y is a parameter (a risk or a random quantity) to be forecasted then the Esscher premium is given by

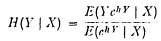
That is, H(Y ∣ X) is the Bayes decision rule for estimating Y given the data X relative to the loss function

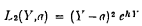
where a is the estimate of Y, and of course the loading h is greater than zero.

Now, for the clincher. This loss function is nonsensical from the point of view of estimation. It indicates a loss (or error) to the forecaster that is essentially the antithesis of relative loss.