Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T20:06:01.166Z Has data issue: false hasContentIssue false
  • English
  • Français

Discussion on D.C.M. Dickson & H.R. Waters Multi-Period Aggregate Loss Distributions for a Life Portfolio

Published online by Cambridge University Press:  29 August 2014

Bjørn Sundt
Bjørn Sundt*
Affiliation:
University of Bergen
*
Vital Forsikring ASA, PO Box 250, N-1326 Lysaker, Norway
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the present discussion we point out the relation of some results in Dickson & Waters (1999) to similar results in Sundt (1998a, b).

We shall need some notation. For a positive integer m let 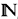m be the set of all m × 1 vectors with positive integer-valued elements and 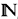m+ = 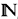m ~ {0}. A vector will be denoted by a bold-face letter and each of its elements by the corresponding italic with a subscript denoting the number of the elements; the subscript · denotes the sum of the elements. Let m0 be the class of probability functions on 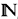m with a positive probability at 0 and 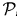m+ the class of probability functions on 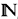m+. For j = 1,…, m we introduce the m × 1 vector ej where the jth element is one and all the other elements zero. We make the convention that summation over an empty range is equal to zero.

Let g ∈ 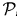m0 be the compound probability function with counting distribution with probability function v ∈ 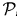10 and severity distribution with probability function h ∈ 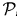m+; we shall denote this compound probability function by v V h. Sundt (1998a) showed that

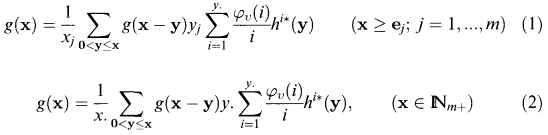
where φv denotes the De Pril transform of v, given by

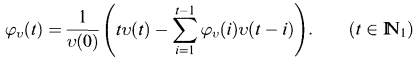
Motivated by (2) Sundt (1998a) defined the De Pril transform φg of g by

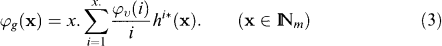
This defines the De Pril transform for all probability functions in m0. Insertion of (2) in (3) gives

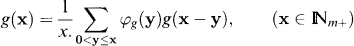
and by solving φg(X) we obtain

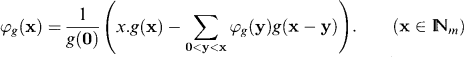
Sundt (1998a) studies the De Pril transform defined in this way and found in particular that it is additive for convolutions.

Type
Articles
Information
ASTIN Bulletin: The Journal of the IAA , Volume 29 , Issue 2 , November 1999 , pp. 311 - 314
Copyright
Copyright © International Actuarial Association 1999

References

De Pril, N. (1989). The aggregate claims distribution in the individual model with arbitrary positive claims. AST1N Bulletin 19, 19–9.Google Scholar
Dhaene, J. & De Pril, N. (1994). On a class of approximative computation methods in the individual model. Insurance: Mathematics and Economics 14, 14–181.Google Scholar
Dhaene, J. & Sundt, B. (1998). On approximating distributions by approximating their De Pril transforms. Scandinavian Actuarial Journal, 1–23.CrossRefGoogle Scholar
Dickson, D.C.M. & Waters, H.R. (1999). Multi-period aggregate loss distributions for a life portfolio. ASTIN Bulletin 29, *–*.CrossRefGoogle Scholar
Sundt, B. (1998a). The multivariate De Pril transform. Research paper 59, Centre for Actuarial Studies, University of Melbourne.Google Scholar
Sundt, B. (1998b). On error bounds for multivariate distributions. Research paper 60, Centre for Actuarial Studies, University of Melbourne.Google Scholar