Christofides (1998) studies the proportional hazards (PH) transform of Wang (1995) and shows that for some parametric families, the PH premium principle reduces to the standard deviation (SD) premium principle. Christofides conjectures that for a parametric family of distributions with constant skewness, the PH premium principle reduces to the SD principle. I will show that this conjecture is false in general but that it is true for location-scale families and for certain other families.

Wang's premium principle has been established as a sound measure of risk in Wang (1995, 1996), Wang, Young, and Panjer (1997), and Wang and Young (1998). Determining when the SD premium principle is a special case of Wang's premium principle is important because it will help identify circumstances under which the more easily applied SD premium principle is a reliable measure of risk.

First, recall that a distortion g is a non-decreasing function from [0, 1] onto itself. Wang's premium principle, with a fixed distortion g, associates the following certainty equivalent with a random variable X, (Wang, 1996) and (Denneberg, 1994):

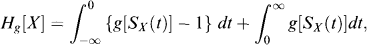
in which Sx is the decumulative distribution function (ddf) of X, Sx(t) = Pr(X > t), t ∈ R. If g is a power distortion, g(p) = pc, then Hg is the proportional hazards (PH) premium principle (Wang, 1995).

Second, recall that a location-scale family of ddfs is 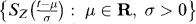, in which Sz is a fixed ddf. Alternatively, if Z has ddf Sz, then {X = μ + σZ: μ∈ R, σ > 0} forms a location-scale family of random variables, and the ddf of 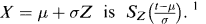. Examples of location-scale families include the normal, Cauchy, logistic, and uniform families (Lehmann, 1991, pp. 20f). In the next proposition, I show that Wang's premium principle reduces to the SD premium principle on a location-scale family. Christofides (1998) observes this phenomenon in several special cases.