Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T14:38:10.069Z Has data issue: false hasContentIssue false
  • English
  • Français

A Characterization of the Esscher-Transformation

Published online by Cambridge University Press:  29 August 2014

Erhard Kremer
Erhard Kremer*
Affiliation:
University of Hamburg, Hamburg, West Germany
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

One of the central problems in risk theory is the calculation of the distribution function F of aggregate claims of a portfolio. Whereas formerly mainly approximation methods could be used, nowadays the increased speed of the computers allows application of iterative methods of numerical mathematics (see Bertram (1981), Küpper (1971) and Strauss (1976)). Nevertheless some of the classical approximation methods are still of some interest, especially a method developed by Esscher (1932).

The idea of this so called Esscher-approximation (see Esscher (1932), Grandell and Widaeus (1969) and Gerber (1980)) is rather simple:

In order to calculate 1 –F(x) for large x one transforms F into a distribution function 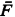such that the mean value of 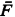is equal to x and applies the Edgeworth expansion to the density of 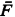The reason for applying the transformation is the fact that the Edgeworth expansion produces good results for x near the mean value, but poor results in the tail (compare also Daniels (1954)).

Type
Research Article
Information
ASTIN Bulletin: The Journal of the IAA , Volume 13 , Issue 1 , June 1982 , pp. 57 - 59
Copyright
Copyright © International Actuarial Association 1982

References

Bertram, J. (1981). Numerische Berechnung von Gesamtschadenverteilungen. Blätter der deutschen Gesellschaft für Versicherungsmathematik, 175–194.Google Scholar
Bühlmann, H. (1980). An economic premium principle. Astin Bulletin, 11, 52–60.CrossRefGoogle Scholar
Daniels, H. E. (1954). Saddlepoint approximations in statistics. Annals of Mathematical Statistics, 631–650.Google Scholar
Esscher, F. (1932). On the probability function in the collective theory of risk. Scandinavian Actuarial Journal, 15, 175–195.Google Scholar
Gerber, H. U. (1980). An Introduction to Mathematical Risk Theory. Huebner Foundation.Google Scholar
Grandell, J. and Widaeus, S. A. (1969). The Esscher approximation method. Scandinavian Actuarial Journal, Supplement, 34–50.CrossRefGoogle Scholar
Kullback, S. (1959). Information Theory and Statistics. Wiley & Sons: New York.Google Scholar
Küpper, J. (1971). Methoden zur Berechnung der Verteilungsfunktion des Totalschadens. Mitteilungen der Vereinigung schweizerischer Versicherungsmathematiker, 279–315.Google Scholar
Strauss, J. (1976). Computerverfahren zur Bestimmung der Gesamtschadenverteilung und ihre Anwendung zur Abschätzung der Großschadenentwicklung. Transactions of the international congress of actuaries, 763–772.Google Scholar