No CrossRef data available.
Article contents
Bayesian Inference in Credibility Theory
Published online by Cambridge University Press: 29 August 2014
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In 1967, Bühlmann has shown that the credibility formula was the best linearized approximation to the exact Bayesian forecast.
His result for the credibility factor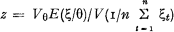 
can be found back by means of some Bayesian inference techniques. Introducing a uniform prior probability density function for the credibility factor provides us with a method for estimating z, a correction term to the Bühlmann's result is obtained. It is shown how prior boundary conditions can be introduced.
- Type
- Research Article
- Information
- Copyright
- Copyright © International Actuarial Association 1975
References
[1]Dr.van Klinken, J. and Drs.Euverman, G. W., Overzicht van de theorie en toepassingen van credibility indices, (unpublished).Google Scholar
[2]Zellner, A. (1971), An Introduction to Bayesian Inference in Econometrics, (eds) John Wiley and Sons, Inc., New York.Google Scholar
[3]Broeckx, F., Goovaerts, M. and van den Broeck, J., On the prior density functions proposed by Jeffreys and Haldane, in a Bayesian framework, Sogesci, to be published.Google Scholar
[4]Jewell, W.S., “The credible distribution”, The ASTIN Bull., Vol. VII, Part 3, pp. 237–269.Google Scholar
[5] For other derivations of the credibility factor see references given by Jewell, W.S. in [4].Google Scholar
[6]BÜhlmann, H. (1970), Mathematical methods in risk theory, (eds) Springer-Verlag, New York.Google Scholar
[7]Bühlmann, H. (1971), Credibility Procedures, Sixth Berkeley Symposium, PP. 515–525.Google Scholar
You have
Access