Article contents
An Economic Premium Principle
Published online by Cambridge University Press: 29 August 2014
Extract
(a) The notion of premium calculation principle has become fairly generally accepted in the risk theory literature. For completeness we repeat its definition:
A premium calculation principle is a functional 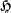 assigning to a random variable X (or its distribution function Fx(x)) a real number P. In symbols
assigning to a random variable X (or its distribution function Fx(x)) a real number P. In symbols

The interpretation is rather obvious. The random variable X stands for the possible claims of a risk whereas P is the premium charged for assuming this risk.
This is of course formalizing the way actuaries think about premiums. In actuarial terms, the premium is a property of the risk (and nothing else), e.g.
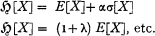
(b) Of course, in economics premiums are not only depending on the risk but also on market conditions. Let us assume for a moment that we can describe the risk by a random variable X (as under a)), describe the market conditions by a random variable Z.
Then we want to show how an economic premium principle
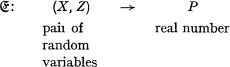
can be constructed. During the development of the paper we will also give a clear meaning to the random variable Z:
In the market we are considering agents i = 1, 2, …, n. They constitute buyers of insurance, insurance companies, reinsurance companies.
Each agent i is characterized by his
utility function ui(x) [as usual: 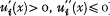 ]
]
initial wealth wi.
In this section, the risk aspect is modelled by a finite (for simplicity) probability space with states s = 1, 2, …, S and probabilities πs of state s happening.
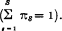
- Type
- Research Article
- Information
- Copyright
- Copyright © International Actuarial Association 1980
References
- 254
- Cited by


