Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T14:37:37.088Z Has data issue: false hasContentIssue false
  • English
  • Français

A GAMMA MOVING AVERAGE PROCESS FOR MODELLING DEPENDENCE ACROSS DEVELOPMENT YEARS IN RUN-OFF TRIANGLES

Published online by Cambridge University Press:  04 November 2020

Luis E. Nieto-Barajas Open the ORCID record for Luis E. Nieto-Barajas [Opens in a new window]  and
Rodrigo S. Targino Open the ORCID record for Rodrigo S. Targino [Opens in a new window]
Luis E. Nieto-Barajas*
Affiliation:
Department of Statistics, Instituto Tecnológico Autónomo de México (ITAM), Mexico City, Mexico E-Mail: [email protected]
Rodrigo S. Targino
Affiliation:
School of Applied Mathematics, Fundação Getulio Vargas (FGV), Rio de Janeiro, Brazil E-Mail: [email protected]
*
E-Mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We propose a stochastic model for claims reserving that captures dependence along development years within a single triangle. This dependence is based on a gamma process with a moving average form of order 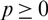$p \ge 0$ which is achieved through the use of poisson latent variables. We carry out Bayesian inference on model parameters and borrow strength across several triangles, coming from different lines of businesses or companies, through the use of hierarchical priors. We carry out a simulation study as well as a real data analysis. Results show that reserve estimates, for the real data set studied, are more accurate with our gamma dependence model as compared to the benchmark over-dispersed poisson that assumes independence.

Keywords

Claims reservinggamma processIncurred But Not Reportedlatent variablesmoving average processesC110C130C320C530
Type
Research Article
Information
ASTIN Bulletin: The Journal of the IAA , Volume 51 , Issue 1 , January 2021 , pp. 245 - 266
Copyright
© 2020 by Astin Bulletin. All rights reserved

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonio, K. and Beirlant, J. (2008) Issues in claims reserving and credibility: A semiparametric approach with mixed models. Journal of Risk and Insurance, 75(3), 643–676.CrossRefGoogle Scholar
Avanzi, B., Taylor, G., Vu, P.A. and Wong, B. (2016) Stochastic loss reserving with dependence: A flexible multivariate Tweedie approach. Insurance: Mathematics and Economics, 71, 63–78.Google Scholar
Avanzi, B., Taylor, G., Vu, P.A. and Wong, B. (2020) A multivariate evolutionary generalised linear model framework with adaptive estimation for claims reserving. Insurance: Mathematics and Economics, 93, 50–71.Google Scholar
de Alba, E. (2002) Bayesian estimation of outstanding claims reserves. North American Actuarial Journal, 6(4), 1–20.CrossRefGoogle Scholar
de Alba, E. and Nieto-Barajas, L.E. (2008) Claims reserving: A correlated Bayesian model. Insurance: Mathematics and Economics, 43(3), 368–376.Google Scholar
De Jong, P. (2006) Forecasting runoff triangles. North American Actuarial Journal, 10(2), 28–38.CrossRefGoogle Scholar
Ecb. (2009) Directive 2009/138/EC of the European parliament and of the council of 25 November 2009 on the taking-up and pursuit of the business of Insurance and Reinsurance (Solvency II). Technical report.Google Scholar
England, P.D. and Verrall, R.J. (2002) Stochastic claims reserving in general insurance. British Actuarial Journal, 8(3), 443–518.CrossRefGoogle Scholar
Finma. (2007) Technical document on the Swiss Solvency Test. Technical report.Google Scholar
Gao, G. (2018) Bayesian chain ladder models. In Bayesian Claims Reserving Methods in Non-life Insurance with Stan, pp. 73–115. Springer.CrossRefGoogle Scholar
Gao, G. and Meng, S. (2018) Stochastic claims reserving via a bayesian spline model with random loss ratio effects. ASTIN Bulletin, 48(1), 55–88.CrossRefGoogle Scholar
Gesmann, M., Murphy, D., Zhang, Y.(W.), Carrato, A., Wuthrich, M., Concina, F. and Dal Moro, E. (2018) ChainLadder: Statistical Methods and Models for Claims Reserving in General Insurance. R package version 0.2.7.Google Scholar
Gisler, A. (2006) The estimation error in the chain-ladder reserving method: A Bayesian approach. Astin Bulletin, 36(02), 554–565.CrossRefGoogle Scholar
Gisler, A. and Wüthrich, M.V. (2008) Credibility for the chain ladder reserving method. Astin Bulletin, 38(02), 565–600.CrossRefGoogle Scholar
Guszcza, J. (2008) Hierarchical growth curve models for loss reserving. In CAS Forum, pp. 146–173.Google Scholar
Ibrahim, J.G. and Laud, P.W. (1994) A predictive approach to the analysis of designed experiments. Journal of the American Statistical Association, 89, 309–319.CrossRefGoogle Scholar
Kremer, E. (2005). The correlated chain-ladder method for reserving in case of correlated claims developments. Blätter DGVFM, 27, 315–322. https://doi.org/10.1007/BF02808313 CrossRefGoogle Scholar
Lally, N. and Hartman, B. (2018) Estimating loss reserves using hierarchical Bayesian Gaussian process regression with input warping. Insurance: Mathematics and Economics, 82, 124–140.Google Scholar
Mack, T. (1993) Distribution-free calculation of the standard error of chain ladder reserve estimates. Astin Bulletin, 23(02), 213–225.CrossRefGoogle Scholar
Merz, M. and Wüthrich, M.V. (2010) Paid–incurred chain claims reserving method. Insurance: Mathematics and Economics, 46(3), 568–579.Google Scholar
Merz, M. and Wüthrich, M.V. (2015) Claims run-off uncertainty: The full picture. Available at SSRN 2524352, version of 3/Jul/2015.Google Scholar
Merz, M., Wüthrich, M.V. and Hashorva, E. (2013) Dependence modelling in multivariate claims run-off triangles. Annals of Actuarial Science, 7(1), 3–25.CrossRefGoogle Scholar
Meyers, G. (2009) Stochastic loss reserving with the collective risk model. Variance, 3(2), 239–269.Google Scholar
Meyers, G. (2015) Stochastic Loss Reserving Using Bayesian MCMC Models. New York: Casualty Actuarial Society.Google Scholar
Meyers, G.G. and Shi, P. (2011) The retrospective testing of stochastic loss reserve models. In Casualty Actuarial Society E-Forum, Summer.Google Scholar
Ntzoufras, I. and Dellaportas, P. (2002) Bayesian modeling of outstanding liabilities incorporating claim count uncertainty. North American Actuarial Journal, 6(1), 113–136.CrossRefGoogle Scholar
Ohlsson, E. and Lauzeningks, J. (2009) The one-year non-life insurance risk. Insurance: Mathematics and Economics, 45(2), 203–208.Google Scholar
Peters, G.W., Dong, A.X.D. and Kohn, R. (2014) A copula based Bayesian approach for paid–incurred claims models for non-life insurance reserving. Insurance: Mathematics and Economics, 59, 258–278.Google Scholar
Peters, G.W., Shevchenko, P.V. and Wüthrich, M.V. (2009) Model uncertainty in claims reserving within Tweedie’s compound Poisson models. ASTIN Bulletin, 39(1), 1–33.CrossRefGoogle Scholar
Pinheiro, P.J.R., Andrade e Silva, J.M. and Centeno, M.L. (2003) Bootstrap methodology in claim reserving. The Journal of Risk and Insurance, 70, 701–714.CrossRefGoogle Scholar
Plummer, M. (2018) rjags: Bayesian Graphical Models using MCMC. R package version 4-8.Google Scholar
Renshaw, A.E. and Verrall, R.J. (1998) A stochastic model underlying the chain-ladder technique. British Actuarial Journal, 4(4), 903–923.CrossRefGoogle Scholar
Shi, P. (2017) A multivariate analysis of intercompany loss triangles. Journal of Risk and Insurance, 84(2), 717–737.CrossRefGoogle Scholar
Shi, P., Basu, S. and Meyers, G.G. (2012) A Bayesian log-normal model for multivariate loss reserving. North American Actuarial Journal, 16(1), 29–51.CrossRefGoogle Scholar
Shi, P. and Hartman, B.M. (2016) Credibility in loss reserving. North American Actuarial Journal, 20(2), 114–132.CrossRefGoogle Scholar
Smith, A.F.M. and Roberts, G.O. (1993) Bayesian computation via the Gibbs sampler and related Markov chain Monte Carlo methods. Journal of the Royal Statistical Society: Series B, 55(1), 3–23.Google Scholar
Spiegelhalter, D.J., Best, N.G., Carlin, B.P. and van der Linde, A. (2002) Bayesian measures of model complexity and fit (with discussion). Journal of the Royal Statistical Society, Series B, 64, 583–639.CrossRefGoogle Scholar
Sriram, K. and Shi, P. (to appear) Stochastic loss reserving: A new perspective from a Dirichlet model. Journal of Risk and Insurance. https://doi.org/10.1111/jori.12311 CrossRefGoogle Scholar
Tanner, M.A. (1991) Tools for Statistical Inference: Observed Data and Data Augmentation Methods. New York: Springer.CrossRefGoogle Scholar
Taylor, G. (2015) Bayesian chain ladder models. Astin Bulletin, 45(01), 75–99.CrossRefGoogle Scholar
Taylor, G. (2012) Loss Reserving: An Actuarial Perspective. Vol. 21. New York: Springer Science & Business Media.Google Scholar
Tierney, L. (1994) Markov chains for exploring posterior distributions. Annals of Statistics, 22, 1701–1728.CrossRefGoogle Scholar
Verrall, R.J. (1991) On the estimation of reserves from loglinear models. Insurance: Mathematics and Economics, 10, 75–80.Google Scholar
Wüthrich, M.V. (2010) Accounting year effects modeling in the stochastic Chain Ladder reserving method. North American Actuarial Journal, 14, 235–255.CrossRefGoogle Scholar
Wuthrich, M.V. (2019) Non-life insurance: mathematics & statistics. Available at SSRN 2319328.Google Scholar
Zhang, Y. and Dukic, V. (2013) Predicting multivariate insurance loss payments under the bayesian copula framework. Journal of Risk and Insurance, 80(4), 891–919.CrossRefGoogle Scholar
Zhang, Y., Dukic, V. and Guszcza, J. (2012) A Bayesian non-linear model for forecasting insurance loss payments. Journal of the Royal Statistical Society: Series A (Statistics in Society), 175(2), 637–656.CrossRefGoogle Scholar