I. INTRODUCTION
The psychovisual process of image quality assessment (IQA) is an interaction between the human visual system (HVS) and the visual stimuli [Reference Wang and Bovik2]. For visual communication systems, visual stimuli is generally a combination of the meaningful image contents and the inevitably introduced noises or artifacts during acquisition, compression, and transmission. According to the psychophysical study of human sensory-threshold [Reference Levine3], for visual stimuli, the inherent artifacts can be classified into three categories [Reference Hay and Chesters4,Reference Lu, Lin, Yang, Ong and Yao5]: Imperceptible noise or subthreshold noise is considered invisible to the HVS and is therefore often out of the question for visual quality assessment. Near-threshold noise is observable to the HVS, and it may obscure some fine image structures but does not obstacle the process of visual recognition. Suprathreshold noise is so intensive that it overwhelms some key image structures and features that are essential for visual perception. The threshold-related behavior of visual perception has a physiological explanation that the HVS has a set of sensory neurons being tuned to specific orientations and frequencies [Reference Valois and Valois6], and the excitation of some neurons may reduce the activity of others. This effect is also known as lateral inhibition [Reference Bekesy7,Reference Orchard and Phillips8].
It has long been realized that near- and suprathreshold visual stimuli should be discriminated since the psychovisual processes involved are quite different [Reference Cornsweet10–Reference Sagi and Hochstein12]. The psychological studies of the “priming” effect of human vision confirm that viewing context can have substantial impacts on visual perception [Reference Kolb and Whishaw13]. In the premise of threshold-related visual perception, it is easy to imagine that the process of visual quality assessment will also be affected by the visibility level of the noise or artifacts. For images containing near-threshold noise, the IQA process of the HVS is a task of detecting artifacts and distortions from the observation. The image quality is better if less artifact can be detected. On the other hand, for images contaminated by suprathreshold noise, subjective IQA becomes a work of inferring meaningful image structures using past experience and prior knowledge. The image quality is better if more significant structures can be discovered.
Although apparent gap exists between near- and suprathreshold IQA, currently there lacks the effective IQA method to account for the difference between near- and suprathreshold noise conditions. And most of existing quality metrics try to handle all noise and artifact levels irrespective of the physiological and psychological differences between near- and suprathreshold noise conditions mentioned above. For the problem of blind (no-reference) IQA, since no information about the original image is available, both the artifacts and meaningful image features have to be detected and discovered solely from the noisy observations. Therefore, the discrimination between near- and suprathreshold noise conditions becomes even more imperative. In this work, we propose a dual-model approach to quality assessment of noisy images under near- and suprathreshold noise conditions. For theoretical simplicity and operational amenability, our study in this work is focused on additive Gaussian white noise (AGWN), which is considered as one of the most simple type of distortions because the noisy signals are independent among pixels. Although being straightforward by itself, AGWN is often considered as a building component for other more complicated distortion types [Reference Sheikh, Bovik and de Veciana14–Reference Wang and Li16]. For example, impacts of quantization noises on perceptual quality can be modeled using Gaussian blurring plus AGWN as introduced in [Reference Sheikh, Bovik and de Veciana14]. This is part of the reason why AGWN has been widely studied in the literature of IQA [Reference Sheikh, Wang, Cormack and Bovik9,Reference Larson and Chandler17,Reference Ponomarenko, Lukin, Zelensky, Egiazarian, Carli and Battisti18]. The study of AGWN can therefore serve as a pilot for the research of other more complicated types of distortions.
For near-threshold AGWN, it will be shown that high correlation exists between subjective quality score and strength (variance) of the noise. This coincides with our conjecture above that IQA is a noise detection/estimation problem under near-threshold conditions. So the near-threshold model of the proposed approach is based on a noise estimation algorithm using natural scene statistics. As aforementioned, for suprathreshold AGWN, IQA transfers to the problem of recovering original image structures from noisy observations. This echoes the general belief that vision is a process of inference, making assumptions and drawing conclusions based on experiences [Reference von Helmholtz19,Reference Sternberg20], or using an internal generative model [Reference Knill and Pouget21–Reference Friston23]. Therefore a Bayesian brain theory [Reference Knill and Pouget21] inspired the inference method based on the free-energy principle [Reference Friston, Kilner and Harrison22,Reference Friston23] will be used as the suprathreshold model of the proposed blind IQA scheme. A mathematical transformation will be used to calibrate the estimates from the near- and suprathreshold models and drive the dual-model distortion metric (DMDM) for blind quality assessment. Plot of the proposed dual-model approach to quality assessment of noisy images is illustrated in Fig. 1. We emphasize that the scope of this paper is beyond the mere introduction of a new blind image quality metric. The dual-model approach combining an artifact detection stage and an active inference stage presented in this paper should be applicable to the general problem of perceptual modeling and perceptual quality assessment and is expected to facilitate future research in the field.

Fig. 1. IQA in the near- and suprathreshold conditions (noisy images taken from LIVE database [9]).
The rest of the paper is organized as follows: Section II introduces the near- and suprathreshold models of the proposed dual-model approach in detail. Section III deals with the unification of the two models. Section IV provides the experimental results and comparative studies. Finally, Section V concludes the paper.
II. DMDM FOR BLIND QUALITY ASSESSMENT
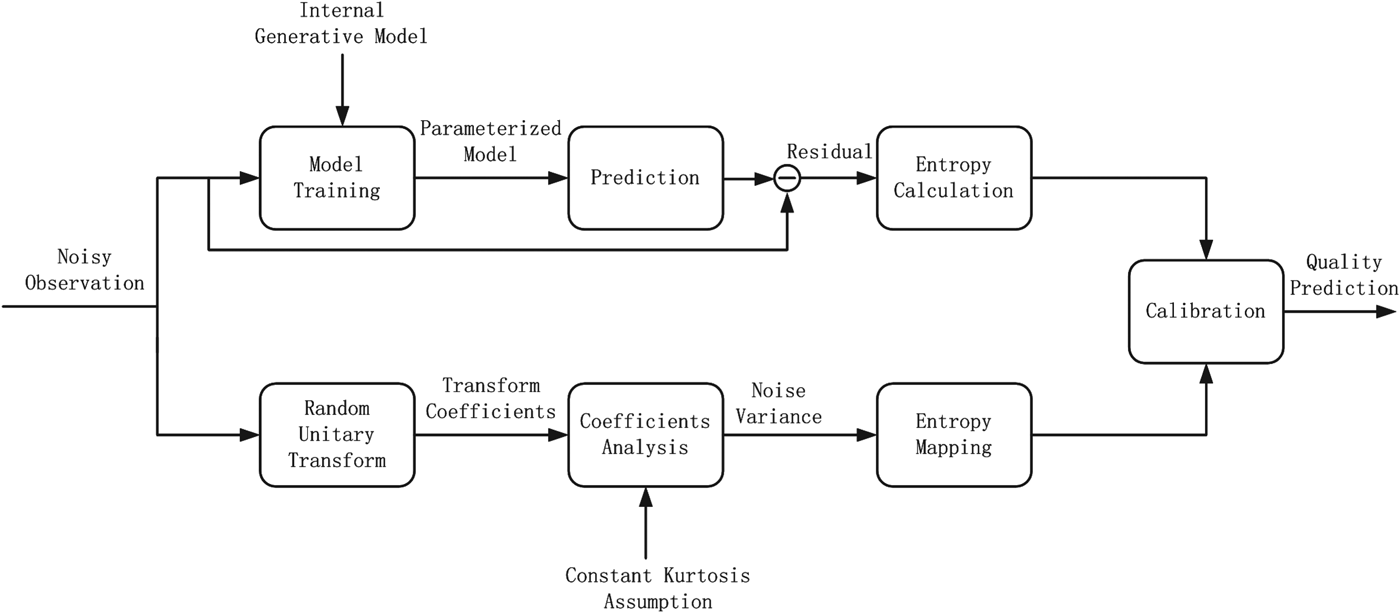
System diagram of the proposed DMDM for blind quality assessment is illustrated in Fig. 2, wherein the near-threshold model based on noise estimation using natural image statistics and the suprathreshold model based on image feature inference using the free-energy principle will be introduced in detail in Sections II-A and II-B, respectively.

Fig. 2. Block diagram of the dual-model approach for blind quality assessment of noisy images.
A) Near-threshold model: noise estimation using natural image statistics
Assuming an additive noise model Y=X+N in the pixel domain, where X is the original image, N is the noise and Y is the noisy observation of X. If X and N are independent, then in the transform domain we also have
where x and y are the transformation of X and Y, and n is the noise in transform domain. Note that N and n will have the same variance, as long as the transform is unitary. It has been discovered that the high-order statistics (e.g. Kurtosis) of transform coefficients of natural images are stable across different frequency indexes [Reference Simoncelli and Olshausen24–Reference Geisler27], which can be used for noise variance estimation.
Kurtosis of x is defined as the fourth cumulant divided by the square of the second cumulant, which equals the normalized fourth central moments minus 3
From the relationship between cumulant and the central moments ![]() $k_{4}(\cdot)=\mu_{4}(\cdot)-3\sigma^{4}(\cdot)$ we have
$k_{4}(\cdot)=\mu_{4}(\cdot)-3\sigma^{4}(\cdot)$ we have
 $$\eqalign{\mu_4(y)&=k_4(y)+3\sigma^4(y) \cr &=k_4(x)+k_4(n)+3\sigma^4(y) \cr &=\mu_4(x)-3\sigma^4(x) +\mu_4(n)-3\sigma^4(n) + 3\sigma^4(y) \cr &={K}(x)\sigma^4(x) + {K}(n)\sigma^4(n) + 3\sigma^4(y),}$$
$$\eqalign{\mu_4(y)&=k_4(y)+3\sigma^4(y) \cr &=k_4(x)+k_4(n)+3\sigma^4(y) \cr &=\mu_4(x)-3\sigma^4(x) +\mu_4(n)-3\sigma^4(n) + 3\sigma^4(y) \cr &={K}(x)\sigma^4(x) + {K}(n)\sigma^4(n) + 3\sigma^4(y),}$$
where we used the fact that x and n are independent. From (2) we have ![]() $\mu_{4}(\cdot) = ({K}(\cdot)+3) \sigma^{4}(\cdot)$, and letting this into (3) we further have
$\mu_{4}(\cdot) = ({K}(\cdot)+3) \sigma^{4}(\cdot)$, and letting this into (3) we further have
which reveals that kurtosis of y are essentially weighted averages of that of x and n and the weights are determined by the ratios between the standard deviation of signals. Again, from the independence between x and y, we have ![]() $\sigma^{2}(y)=\sigma^{2}(x)+\sigma^{2}(n)$, letting which into (4), we arrive at
$\sigma^{2}(y)=\sigma^{2}(x)+\sigma^{2}(n)$, letting which into (4), we arrive at
 $${K}(y)= \left({\sigma^2(y)-\sigma^2(n) \over \sigma^2(y)} \right)^2{K} (x) + \left({\sigma^2(n) \over \sigma^2(y)} \right)^2 {K}(n),$$
$${K}(y)= \left({\sigma^2(y)-\sigma^2(n) \over \sigma^2(y)} \right)^2{K} (x) + \left({\sigma^2(n) \over \sigma^2(y)} \right)^2 {K}(n),$$which enables us to quantify the relationships between the kurtosis of the original and the noisy transformed signals using the second moments (variances) of the noise n and the noisy observation y.
Recently, Zoran and Weiss [Reference Zoran and Weiss28] propose to estimate noise variance by applying the equation (5) upon multiple subbands of discrete cosine transform (DCT) coefficients of the noisy images. However, Zhai and Wu's work [Reference Zhai and Wu29] suggests that the dominant horizontal and vertical edges in images may lead to a violation of the scale invariance assumption for DCT subbands [Reference Srivastava, Lee, Simoncelli and Zhu25,Reference Mumford, Haykin, Principe, Sejnowski and McWhirter26]. On the other hand, Huang [Reference Huang and Mumford30,Reference Huang31] first noticed that random transform coefficients of natural images have high kurtosis. In addition, the research in [Reference Zhai and Wu29] validate that for random transform coefficients the kurtosis is not only high but also remains approximately a constant, which is a very useful property in estimating noise variance, and to preserve the noise energy in the transform domain, a unitary transform has to be used. For a k×k data matrix A, its two-dimensional (2D) random unitary transform (RUT) [Reference Zhai and Wu29] can be computed as follows: we first compute the QR decomposition of a k×k random matrix C as QR=C. We then extract the diagonal elements of the upper triangular matrix ![]() $V=\hbox{diag}(R)$ and normalize it as
$V=\hbox{diag}(R)$ and normalize it as ![]() ${\cal V} = V/\vert V \vert$. A new upper triangular matrix is formed as
${\cal V} = V/\vert V \vert$. A new upper triangular matrix is formed as ![]() $R^{\prime}=\hbox{diag}({\cal V})$ and the RUT matrix is computed as T=QR′. The unitary of T is obvious since
$R^{\prime}=\hbox{diag}({\cal V})$ and the RUT matrix is computed as T=QR′. The unitary of T is obvious since ![]() $T^{T}T=(QR^{\prime})^{T}QR^{\prime} = R^{\prime T} R^{\prime} = I_{k}$, where we use the fact that R′ is a diagonal matrix with normalized entries. The 2D RUT for A can then be computed as B=TAT T.
$T^{T}T=(QR^{\prime})^{T}QR^{\prime} = R^{\prime T} R^{\prime} = I_{k}$, where we use the fact that R′ is a diagonal matrix with normalized entries. The 2D RUT for A can then be computed as B=TAT T.
By employing (5) on the subbands of the RUT coefficients, we can estimate the noise variance by solving the following constrained nonlinear programming problems:
 $$\eqalign{&\widehat{{K}}(x), \widehat{{K}}(n), \widehat{\sigma}^2(n) =\mathop{\arg\,\min}_{{K}(x), {K}(n), \sigma^2(n)} \sum_{i\in \cal I} \cr &\left\Vert \widehat{{K}}(y_i)- \left ({\widehat{\sigma}^2(y_i)-\sigma^2(n) \over \widehat{\sigma}^2(y_i)}\right )^{2}{K}(x)+\left({\sigma^2(n) \over \widehat{\sigma}^2(y_i)}\right)^{2}{K}(n)\right\Vert_1 \cr &\hbox{subject to} {K}(x),{K}(n) \geq -2,}$$
$$\eqalign{&\widehat{{K}}(x), \widehat{{K}}(n), \widehat{\sigma}^2(n) =\mathop{\arg\,\min}_{{K}(x), {K}(n), \sigma^2(n)} \sum_{i\in \cal I} \cr &\left\Vert \widehat{{K}}(y_i)- \left ({\widehat{\sigma}^2(y_i)-\sigma^2(n) \over \widehat{\sigma}^2(y_i)}\right )^{2}{K}(x)+\left({\sigma^2(n) \over \widehat{\sigma}^2(y_i)}\right)^{2}{K}(n)\right\Vert_1 \cr &\hbox{subject to} {K}(x),{K}(n) \geq -2,}$$
where ![]() $\cal I$ denotes the set of frequency indexes of RUT and the constraints are from the definition of Kurtosis. We emphasize that the analysis in this section is only based on the independent additive noise model as given in (1), and there is no underlying assumption about the distributions of transform coefficients x and n.
$\cal I$ denotes the set of frequency indexes of RUT and the constraints are from the definition of Kurtosis. We emphasize that the analysis in this section is only based on the independent additive noise model as given in (1), and there is no underlying assumption about the distributions of transform coefficients x and n.
B) Suprathreshold model: structure inference with generative model
Recently, Friston [Reference Friston, Kilner and Harrison22,Reference Friston23] proposed the free-energy principle to explain and unify several brain theories in biological and physical sciences about human action, perception, and learning. Similar to the Bayesian brain hypothesis, a basic premise of the free energy-based brain theory is that the cognitive process is governed by an internal generative model. Using the generative model, human brain renders predictions of those encountered scenes in a constructive manner, and the constructive model is essentially a probabilistic model that decomposes into a likelihood term and a prior term. Visual perception is then the process of inverting this likelihood term so as to infer the posterior possibilities of the given scene. Not surprisingly, since the internal generative model cannot be universal (implying the limitation of one's knowledge and experience), there always exists a gap between the encountered scene and brain's prediction. As mentioned in the Introduction section, for images with suprathreshold noise, features, and cues that are essential for visual perception are overwhelmed, so visual perception reasonably follows the manner of inference as outline by the free-energy principle, and under those conditions, the gap between the external input and its generative-model-explainable part is intimately related to the quality of perceptions and therefore determines the perceptual quality of the image.
For operational amenability, we assume that the internal generative model ![]() $\cal{G}$ for visual perception is parametric, which explains perceived scenes by adjusting the vector
$\cal{G}$ for visual perception is parametric, which explains perceived scenes by adjusting the vector ![]() ${\bf \theta}$ of parameters. Given a visual stimuli, or an image I, its “surprise” (measured by entropy) can be computed by integrating the joint distribution
${\bf \theta}$ of parameters. Given a visual stimuli, or an image I, its “surprise” (measured by entropy) can be computed by integrating the joint distribution ![]() $P(I,{\bf \theta} \vert \cal{G})$ over the space of model parameters
$P(I,{\bf \theta} \vert \cal{G})$ over the space of model parameters ![]() ${\bf \theta}$
${\bf \theta}$
We further introduce an auxiliary term ![]() $Q({\bf \theta} \vert I)$ into both the denominator and numerator in (7) and have
$Q({\bf \theta} \vert I)$ into both the denominator and numerator in (7) and have
Here ![]() $Q({\bf \theta} \vert I)$ is a posterior distribution of the model parameters given the image. It can be thought of as an approximate posterior to the true posterior of the model parameters
$Q({\bf \theta} \vert I)$ is a posterior distribution of the model parameters given the image. It can be thought of as an approximate posterior to the true posterior of the model parameters ![]() $P({\bf \theta} \vert I,\cal{G})$ that can be calculated by the brain. The brain minimizes the discrepancy between the approximate posterior
$P({\bf \theta} \vert I,\cal{G})$ that can be calculated by the brain. The brain minimizes the discrepancy between the approximate posterior ![]() $Q({\bf \theta} \vert I,\cal{G})$ and the true posterior
$Q({\bf \theta} \vert I,\cal{G})$ and the true posterior ![]() $P({\bf \theta} \vert I,\cal{G})$ when perceiving I, or adjusting the parameters
$P({\bf \theta} \vert I,\cal{G})$ when perceiving I, or adjusting the parameters ![]() ${\bf \theta}$ of
${\bf \theta}$ of ![]() $Q({\bf \theta} \vert I,\cal{G})$ to best explain I. Therefore, it is also called the recognition density in Bayesian brain theory [Reference Knill and Pouget21]. Note that in (8), the negative “surprise”
$Q({\bf \theta} \vert I,\cal{G})$ to best explain I. Therefore, it is also called the recognition density in Bayesian brain theory [Reference Knill and Pouget21]. Note that in (8), the negative “surprise” ![]() $\log P(I \vert \cal{G})$ is also known as the log-evidence of the image data I given the model. Clearly, the minimization of surprise equals the maximization of model evidence. In our analysis below, the dependency on the generative model
$\log P(I \vert \cal{G})$ is also known as the log-evidence of the image data I given the model. Clearly, the minimization of surprise equals the maximization of model evidence. In our analysis below, the dependency on the generative model ![]() $\cal{G}$ is dropped for simplicity. Using Jensen's inequality, from (8) we have
$\cal{G}$ is dropped for simplicity. Using Jensen's inequality, from (8) we have
and the right-hand side which is defined as the free energy
By letting ![]() $P(I,{\bf \theta})= P({\bf \theta} \vert I)P(I)$ into (10) we have
$P(I,{\bf \theta})= P({\bf \theta} \vert I)P(I)$ into (10) we have
 $$\eqalign{F({\bf \theta})&=\int Q({\bf \theta} \vert I)\log {Q({\bf \theta} \vert I) \over P({\bf \theta} \vert I)P(I)} d{\bf \theta} \cr &=-\log P(I)+\int Q({\bf \theta} \vert I)\log {Q({\bf \theta} \vert I) \over P({\bf \theta} \vert I)}d{\bf \theta} \cr &=-\log P(I) + KL\lpar Q({\bf \theta} \vert I)\Vert P({\bf \theta} \vert I)\rpar .}$$
$$\eqalign{F({\bf \theta})&=\int Q({\bf \theta} \vert I)\log {Q({\bf \theta} \vert I) \over P({\bf \theta} \vert I)P(I)} d{\bf \theta} \cr &=-\log P(I)+\int Q({\bf \theta} \vert I)\log {Q({\bf \theta} \vert I) \over P({\bf \theta} \vert I)}d{\bf \theta} \cr &=-\log P(I) + KL\lpar Q({\bf \theta} \vert I)\Vert P({\bf \theta} \vert I)\rpar .}$$
According to Gibbs’ inequality, the Kullback–Leibler divergence ![]() $KL(\cdot \vert \vert \cdot)$ between the recognition (approximate) posterior and true posterior parameter distribution in (11) is non-negative, i.e.
$KL(\cdot \vert \vert \cdot)$ between the recognition (approximate) posterior and true posterior parameter distribution in (11) is non-negative, i.e. ![]() $KL\lpar Q({\bf \theta} \vert I)\Vert P({\bf \theta} \vert I)\rpar \geq 0$, with equality if and only if
$KL\lpar Q({\bf \theta} \vert I)\Vert P({\bf \theta} \vert I)\rpar \geq 0$, with equality if and only if ![]() $Q({\bf \theta} \vert I) = P({\bf \theta} \vert I)$. Here the free energy F(θ) defines a strict upper bound of the “surprise” or negative model evidence. As indicated in (11), for fixed image data I, the free energy is suppressed by minimizing the divergence term. In other words, the brain tries to lower the divergence
$Q({\bf \theta} \vert I) = P({\bf \theta} \vert I)$. Here the free energy F(θ) defines a strict upper bound of the “surprise” or negative model evidence. As indicated in (11), for fixed image data I, the free energy is suppressed by minimizing the divergence term. In other words, the brain tries to lower the divergence ![]() $KL\lpar Q({\bf \theta} \vert I)\Vert P({\bf \theta} \vert I)\rpar $ between the approximate recognition density of model parameters and its true posterior density when perceiving a given scene. And following the analysis we made at the beginning of this subsection, the computed free-energy term can be used directly as a no reference measure of image quality. For a clean image with little noise contamination, an ideal generative model is expected to recognize the essential image features well and the free energy will be low, indicating a higher image quality. While for noisy image with perceptually important features being besmirched, the free energy induced the generative model will be high, indicating a lower perceptual quality.
$KL\lpar Q({\bf \theta} \vert I)\Vert P({\bf \theta} \vert I)\rpar $ between the approximate recognition density of model parameters and its true posterior density when perceiving a given scene. And following the analysis we made at the beginning of this subsection, the computed free-energy term can be used directly as a no reference measure of image quality. For a clean image with little noise contamination, an ideal generative model is expected to recognize the essential image features well and the free energy will be low, indicating a higher image quality. While for noisy image with perceptually important features being besmirched, the free energy induced the generative model will be high, indicating a lower perceptual quality.
In practice, the internal generative model can be further simplified as a linear model such as the noncausal autoregressive (AR) model and the linear AR model can be locally optimized from the observation. Some implementation details will be briefly introduced in the next section and more theoretical treatments regarding the free-energy principle and the approximation using an AR model can be found in [Reference Zhai, Wu, Yang, Lin and Zhang32]. The calibration and combination of the near- and suprathreshold models toward a final dual-model quality metric will be discussed in the next section.
III. MODEL CALIBRATION AND INTEGRATION
The near- and suprathreshold quality metrics based on natural image statistics and the free-energy principle have been introduced in Sections II-A and II-B, respectively. For near-threshold quality assessment, the noise estimation is used as a distortion measure, whereas for suprathreshold quality assessment, the free energy of the noisy observation is used as a distortion measure. Obviously, the noise strength measure by variance and free-energy measure by entropy are of different dimension so the two-quality model cannot be combined directly, and this section discusses the unification and calibration of the two distortion measures and defines the so-called DMDM, for blind quality assessment.
Assuming an additive noise model Y=X+N, where ![]() $N\sim \cal{N}(0,\sigma)$ is the Gaussian noise term. For
$N\sim \cal{N}(0,\sigma)$ is the Gaussian noise term. For ![]() $N \sim \psi (n) = (1/\sqrt{2\pi\sigma^{2}}) \times e^{-n^{2}/2\sigma^{2}}$, its differential entropy can be computed as
$N \sim \psi (n) = (1/\sqrt{2\pi\sigma^{2}}) \times e^{-n^{2}/2\sigma^{2}}$, its differential entropy can be computed as
 $$\eqalign{H(\psi) &= -\int \psi (n)\ln \psi (n) dn \cr &=-\int \psi (n) \left(-{n^2 \over 2\sigma^2} - \ln \sqrt{2\pi\sigma^2} \right) dn \cr &= {1 \over 2} + {1 \over 2} \ln 2 \pi \sigma^2 = {1 \over 2} \ln 2 \pi e \sigma^2.}$$
$$\eqalign{H(\psi) &= -\int \psi (n)\ln \psi (n) dn \cr &=-\int \psi (n) \left(-{n^2 \over 2\sigma^2} - \ln \sqrt{2\pi\sigma^2} \right) dn \cr &= {1 \over 2} + {1 \over 2} \ln 2 \pi \sigma^2 = {1 \over 2} \ln 2 \pi e \sigma^2.}$$Note that the entropy in (12) is in nats, and by changing the logarithm base, we get the entropy in bits as
Equation (13) provides a means to convert the estimate from the near-threshold noise estimation model to the entropy-based quality measure as given by the near-threshold quality model
with ![]() $\hat{\sigma}$ being the variance estimate from (6) and Y is the noisy observation.
$\hat{\sigma}$ being the variance estimate from (6) and Y is the noisy observation.
One should excise caution when combining the transformed entropy measure from near-threshold model and the entropy measure from the suprathreshold model. This is because the free-energy value, when being approximated using a locally learnt linear AR model as introduced in Section II-B, contains contributions from the meaningful image structures. Ideally, for a perfect internal generative model, the approximation error of the free-energy model contains only the AGWN. However, in practice, since a linear AR model is used as an delegate of the idealistic internal model and is optimized with the noisy samples, the estimation error inevitably carries some of the image structures and has to be calibrated before model integration.
The linear estimation using a linear AR model from noisy observation Y can be written as
where Y 0 is a vector consists of samples from the neighborhood and A is the coefficient matrix. To minimize the estimation error ![]() $E = Y - \hat{Y}$, from the orthogonal principle, the error must be perpendicular to the observation Y 0. Therefore we have
$E = Y - \hat{Y}$, from the orthogonal principle, the error must be perpendicular to the observation Y 0. Therefore we have
From (16) we can get ![]() $\Sigma_{YY_{0}^{T}} = A\Sigma_{Y_{0}}$, so the optimal linear coefficient matrix is
$\Sigma_{YY_{0}^{T}} = A\Sigma_{Y_{0}}$, so the optimal linear coefficient matrix is
The covariance matrix of error vector E can be written as
 $$\eqalign{\Sigma_{E}&= E[(Y - \hat{Y})(Y - \hat{Y})^T] \cr &= E[(Y - A Y_0)(Y - A Y_0)^T] \cr &= E[(Y - A Y_0)(Y^T - Y_0^T A^T)] \cr &= \Sigma_Y - \Sigma_{YY_0^T} A^T - A \Sigma_{Y_0Y^T} + A\Sigma_{Y_0}A^T.}$$
$$\eqalign{\Sigma_{E}&= E[(Y - \hat{Y})(Y - \hat{Y})^T] \cr &= E[(Y - A Y_0)(Y - A Y_0)^T] \cr &= E[(Y - A Y_0)(Y^T - Y_0^T A^T)] \cr &= \Sigma_Y - \Sigma_{YY_0^T} A^T - A \Sigma_{Y_0Y^T} + A\Sigma_{Y_0}A^T.}$$From (17) we have
And letting (19) into (18) we arrive at
On the other hand, from the independence between Y and N, we have ![]() $\Sigma_{YY_{0}^{T}} = \Sigma_{Y_{0}Y^{T}} = \Sigma_{X}$ and
$\Sigma_{YY_{0}^{T}} = \Sigma_{Y_{0}Y^{T}} = \Sigma_{X}$ and ![]() $\Sigma_{Y} = \Sigma_{X} + \sigma_{n}^{2}I$. Therefore (20) reduces to
$\Sigma_{Y} = \Sigma_{X} + \sigma_{n}^{2}I$. Therefore (20) reduces to
Using the equation of the inverse of sum of matricesFootnote 2 (21) can be further written as
which indicates that the covariance of the residual signal from the linear prediction is larger than that of the noise signal alone, and under the simplest condition of pixel-wise estimation, (22) becomes
where σe2 and σx2 are respectively the variance for the error term and the image signal. Equation (23) indicates that variance of the estimate error of the free-energy model, as computed from a linear AR model, is larger than variance of the inherent AGWN in the observation. Therefore, care should be taken to properly shrink the free-energy term before combining with the estimate from the near-threshold model.
However, a precise correction using (23) requires the variance of the original signal x, which is out of question for blind quality assessment algorithm. In fact, the difference term ![]() $((\sigma_{x}^{2})^{-1} + (\sigma_{n}^{2})^{-1})^{-1}$ in (23) defines a harmonic mean between
$((\sigma_{x}^{2})^{-1} + (\sigma_{n}^{2})^{-1})^{-1}$ in (23) defines a harmonic mean between ![]() $\sigma_{x}^{2}$ and
$\sigma_{x}^{2}$ and ![]() $\sigma_{n}^{2}$. On the other hand, σx2 can change drastically from one location to another due to different local features of the image signal, making the relationship between σe2 and σx2 even more complicated. Fortunately, in practice, on average for the whole image, it is possible to assume a constant shrinkage
$\sigma_{n}^{2}$. On the other hand, σx2 can change drastically from one location to another due to different local features of the image signal, making the relationship between σe2 and σx2 even more complicated. Fortunately, in practice, on average for the whole image, it is possible to assume a constant shrinkage
where F(θ) is the free-energy value computed with a linear AR model using the noisy observation Y. We empirically find ξ=0.89 which gives a reasonably well-calibration result.
To combine the estimates from the near-threshold model in (14) and suprathreshold model in (24) and to derive the final DMDM value H DM, we can simply use a binary integration
where ζ is a predefined switching threshold and we empirically set ζ=6.2 in this research. Note that besides the binary combination scheme used above, other linear/non-linear combinations are also possible.
Matlab code of the proposed DMDM algorithm can be found at multimedia.sjtu.edu.cn.
IV. EXPERIMENTAL RESULTS AND COMPARATIVE STUDY
The test images used in this work are taken from the widely used LIVE database [Reference Sheikh, Wang, Cormack and Bovik9]. Note some of other emerging test databases, such as TID2008 [Reference Ponomarenko, Lukin, Zelensky, Egiazarian, Carli and Battisti18] and CSIQ [Reference Larson and Chandler17] also have subsets of AGWN contaminated images, but the noise levels (variances) used in both TID2008 and CSIQ databases are very limitedFootnote 3, making themselves not suitable for a fair and trustable test of image quality metric based on noise level estimation.
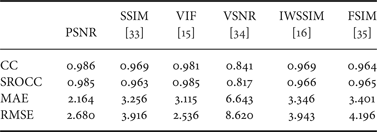
We first report the performances of some classic and contemporary general-purpose full-reference quality metrics on AGWN contaminated images. The full-reference quality metrics tested in this paper include the ubiquitous peak signal-to-noise ratio (PSNR), state-of-the-art SSIM [Reference Wang, Bovik, Sheikh and Simoncelli33], VIF [Reference Sheikh and Bovik15], and VSNR [Reference Chandler and Hemami34], and two of the newest quality metrics IWSSIM [Reference Wang and Li16] and FSIM [Reference Zhang, Zhang, Mou and Zhang35]. Figure 3 shows the scatter plots of scores of the quality metrics versus difference mean opinion score (DMOS) of the test images from the LIVE database. And solid line in those plots is the nonlinear regression curve using the 4 parameter logistic function suggested by the video quality expert group (VQEG) [39]
where s is the input score, while M(s) is the mapped score and β1,…,β4 are free parameters to be determined during the curve-fitting process. The numerical performance analysis suggested by VQEG [39] is provided in Table 1, including four commonly used testing criteria: the correlation coefficient (CC), Spearman rank-order correlation coefficient (SROCC), mean absolute error (MAE) and root-mean-squared error (RMSE). Note that higher correlations and lower mean errors in the table indicate better performance of the quality metric. It can be concluded from Fig. 3 is that the five general-purpose full-reference quality metrics PSNR, SSIM, VIF, IWSSIM, and FSIM all perform fairly well for the IQA of AGWN contaminated images. And the numerical performances in Table 1 indicate that the linear/nonlinear correlations between the IQA scores and the DMOS are as good as 0.96~0.98, much higher than the metrics’ performances on other subset of the LIVE databaseFootnote 4. However, those full-reference quality metrics all require the original pristine images as inputs, which greatly restrains the application scenario, and we will focus on how to design a blind/no-reference quality metric in this work.

Fig. 3. Scatter plots of DMOS/MOS versus full-reference quality metrics on test databases LIVE [9]
Table 1. Comparisons of full-reference image quality metrics on AGWN images in LIVE database.

The scatter plots of DMOS versus some no-reference image quality metrics on the LIVE database are illustrated in Fig. 4. The results of the scale-invariant noise estimation (SINE) i.e. near-threshold model and the no-reference free energy-based distortion metric (NFEDM), i.e. the suprathreshold model are shown respectively in Figs. 4(a) and 4(b). Not surprisingly, the near-threshold model and the suprathreshold model have dissimilar yet complementary performances across different noise levels. It is noticed in Fig. 4(a) that for images of relatively high quality (e.g. DMOS≤45), SINE seems to correlate well the subjective scores, confirming the assumption that for images with near-threshold noise, perceptual quality assessment is process of gauging noise levels. Therefore, image quality can be well approximated through noise estimation. Note that at very low noise levels (e.g. σ≤2.5) the performance of SINE drops because of the possible interference between image signal and noises. Meanwhile, it is found in Fig. 4(b) that NFEDM performs better for images of relatively low quality (e.g. DMOS>45), indicating the plausibility of a free-energy-based inference model for blind quality assessment of images corrupted by suprathreshold noisesFootnote 5. The above observations not only demonstrate the existence of the dissimilar mechanisms of perceptual quality assessment for near- and suprathreshold noise conditions, but also justify the appropriateness of the proposed dual-model approach to IQA combining a noise estimation model and an image inference model. Inheriting merits from both near- and suprathreshold model, the proposed DMDM obviously has a more consistent performance over all noise levels, outperforming both near- and suprathreshold models, as illustrated in Fig. 4(c).

Fig. 4. Scatter plots of DMOS/MOS versus no-reference quality metrics on test databases LIVE [9]
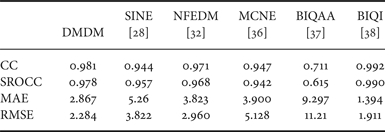
For a thorough comparison, some blind quality metrics, including the mean curvature-based noise estimation (MCNE) [Reference Li36], blind IQA through anisotropy (BIQAA) [Reference Gabarda and Cristóbal37], and the Blind Image Quality Index (BIQI) [Reference Moorthy and Bovik38] are also included in our comparison in Figs. 4(d)–4(f). Note that BIQI is a training-based approach with parameters optimized on the LIVE database itself [Reference Moorthy and Bovik38], so its performance is understandably far better than other metrics. And MCNE and BIQAA are clearly outperformed by the proposed DMDM on a wide quality range. A comparison between proposed DMDM and those full-reference metrics shown in Fig. 3 suggests that though being a no-reference method, DMDM has performance almost equivalent to some of the best full-reference metrics, such as SSIM and VIF.
Numerical performances of the no-reference quality assessment algorithms, using metrics suggested by the VQEG are listed in Table 2. The linear and nonlinear correlation coefficients between DMDM and DMOS are about 0.98, indicating a prediction accuracy comparable with those of PSNR and VIF and superior than SSIM, VSNR, IWSSIM, and FSIM, as listed in Table 1. Moreover, the MAE and RMSE performances of DMDM are even better than those of VIF and most of other full-reference metrics. Again, BIQI results included in Table 2 is just for reference, since BIQI was trained on the LIVE database, and its direct comparison with other metrics is unfair.
Table 2. Comparisons of no-reference image quality metrics on AGWN images in LIVE database.

V. CONCLUSION
Despite all the literatures and discussions of IQA, a fundamental question appear not to have been posed clearly, let alone answered: is there any difference between quality assessment under different noise/artifact levels. In this paper, we demonstrate that there does exist dissimilar psychovisual mechanism of the HVS under near- and suprathreshold noise levels. Taking the artifact of AGWN as an example, we approximate the behavior of HVS using a dual-model approach: a noise estimate model based on natural image statistic for near-threshold noise and an image inference model based on the free-energy principle for suprathreshold noise. We show that the proposed dual-model-based distortion metric outperforms some of state-of-the-art blind and full-reference quality metrics. The proposed dual-model approach to IQA sheds light on the necessity, possibility and effectuality of incorporating cognitive factors into the problem of IQA, and the dual-model framework is also extendable to other more complicated distortion types and is expected to improve the performances of existing image quality metrics that were designed to be universal, handling all noise/artifact levels.
ACKNOWLEDGEMENTS
This paper was supported in part by the National Science Foundation of China under grant number (61371146) and the Humboldt Foundation.
Guangtao Zhai received the Ph.D. degree from Shanghai Jiao Tong University, Shanghai, China in 2009. He was a Humboldt research fellow at the Chair of Multimedia Communications and Signal Processing, Friedrich-Alexander-University, Germany. He is now a Research Professor at Shanghai Jiao Tong University, China. His research interests include multimedia signal processing and perceptual signal processing.
Andre Kaup is a Professor and Head at the Chair of Multimedia Communications and Signal Processing, Friedrich-Alexander-University, Germany. His research interests include image and video signal processing, coding of images, video, and multiview data, as well as multimedia communication.
Jia Wang is an Associate Professor at Shanghai Jiao Tong University, China. His research interests include image processing and information theory.
Xiaokang Yang is a Professor at Shanghai Jiao Tong University, China. His research interests include visual signal processing, machine learning, and pattern recognition.