I. INTRODUCTION
Automatic music transcription (AMT) refers to the estimation of pitches, onset times, and durations of musical notes from music signals and has been considered to be important for music information retrieval. Since multiple pitches usually overlap in polyphonic music and each pitch consists of many overtone components, estimation of multiple pitches is still an open problem. Although such multipitch estimation is often called AMT, quantization of onset times and durations of musical notes is required for completing AMT.
A major approach to multipitch estimation and AMT is to use non-negative matrix factorization (NMF) [Reference Smaragdis and Brown1–Reference Vincent, Bertin and Badeau4]. It approximates the magnitude spectrogram of an observed music signal as the product of a basis matrix (spectral template vectors, each of which corresponds to a pitch) and an activation matrix (gain vectors, each of which is associated with a spectral template). NMF can be interpreted as statistical inference of a generative model that represents the process in which multiple pitches with time-invariant spectra are superimposed to generate an observed audio signal. There remain two major problems when we adopt it for multipitch estimation. First, the estimated activation matrix needs to be thresholded in post-processing to obtain a piano roll that indicates the existence of each pitch at each time unit (e.g., 16th-note length or time frame). An optimal threshold is different for each musical piece and is thus difficult to find. Second, relationships among two or more pitches are not considered in NMF, which may result in musically inappropriate estimations.
When humans manually transcribe music signals into musical scores, not only the audio reproducibility but also musical appropriateness of the scores is considered to avoid musically unnatural notes. Such musical appropriateness can be measured in accordance with a music theory (e.g., counterpoint theory and harmony theory). For instance, music has simultaneous and temporal structures; certain kinds of pitches (e.g., C, G, and E) tend to simultaneously occur to form chords (e.g., C major) and chords vary over time to form typical progressions.
Many studies have been conducted for estimating chords from musical scores [Reference Rocher, Robine, Hanna and Strandh5–Reference Ueda, Uchiyama, Nishimoto, Ono and Sagayama8]. If chord labels are given as clues for multipitch estimation, musically appropriate piano rolls is expected to be obtained. Typical chords and chord progressions, however, vary between music styles, e.g., the harmony theory of jazz music is different from that of classical music. It would thus be better to infer chords and their progressions adaptively for each musical piece. Since chords are determined by note cooccurrences and vice versa, simultaneous estimation of chords and note cooccurrences is a chicken-and-egg problem. This indicates that it is appropriate to estimate chords and note cooccurrences in a unified framework.
In this paper, we propose a novel statistical method that discovers interdependent chords and pitches from music signals in an unsupervised manner (Fig. 1). We formulate a unified probabilistic generative model of a music spectrogram by integrating an acoustic model and a language model in the frame or tatum (16th-note-level beat) level, where the correct tatum times are assumed to be given in this paper. The acoustic model represents how the spectrogram is generated from a piano roll based on an extension of NMF with binary activations of pitches in the same way as [Reference Liang and Hoffman9]. The language model represents how the piano roll is generated from a chord sequence based on an autoregressive hidden Markov model (HMM) that considers the sequential dependencies of chords and pitches. In our previous study [Reference Ojima, Nakamura, Itoyama and Yoshii10], we formulated only a frame-level unified model based on a standard HMM that considers only the sequential dependency of chords.
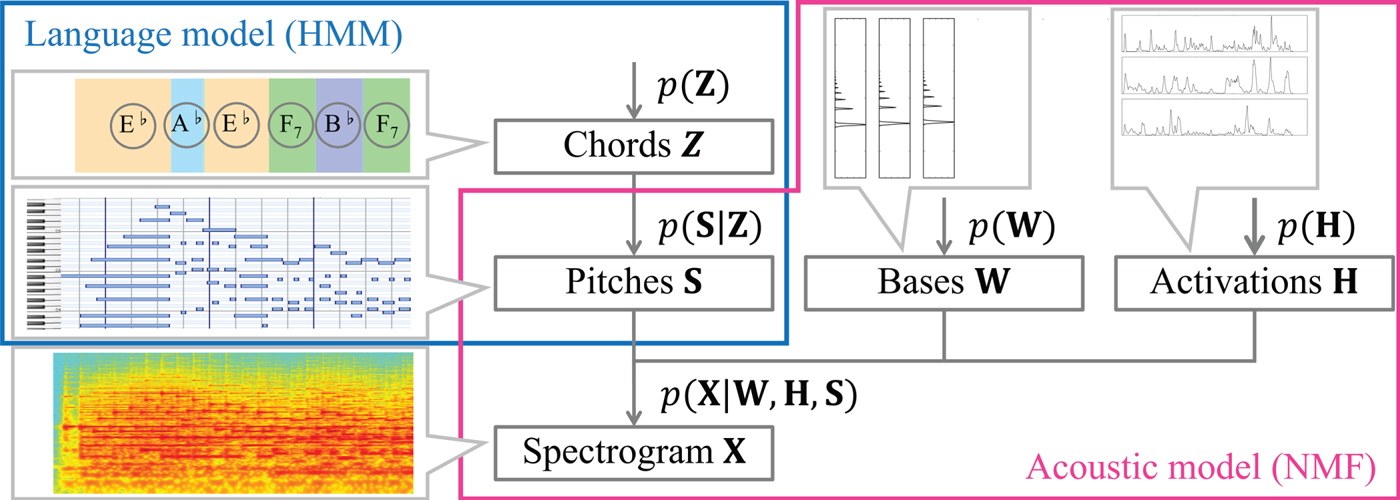
Fig. 1. A hierarchical generative model consisting of language and acoustic models that are linked through binary variables representing the existences of pitches.
We then solve the inverse problem, i.e., given a music spectrogram, the whole model is inferred jointly. Since the acoustic and language models can be trained jointly in an unsupervised manner, the basis spectra of pitched instruments and typical note cooccurrences are learned directly from the observed music signal and all the latent variables (pitches and chords) are thus estimated jointly by using Gibbs sampling. Note that the language model can be trained in advance and the probabilities of typical note cooccurrences obtained from the training data are used as the parameters of the language model.
The major contribution of this study is to achieve grammar induction from music signals by integrating acoustic and language models. Both models are jointly learned in an unsupervised manner unlike a typical approach to automatic speech recognition (ASR). While ASR is based on a two-level hierarchy (word–spectrogram), our model has a three-level hierarchy (chord–pitch–spectrogram) by using an HMM instead of a Markov model (n-gram model) as a language model. We conducted comprehensive comparative experiments to evaluate the effectiveness of each component of the proposed unified model. Another important contribution is to release beat and chord annotations of the MAPS database [Reference Emiya, Badeau and David11] used for evaluation. Recently, ground-truth annotations of several musical elements (e.g., tempo, time signature, and key) for the MAP database were released by Ycart and Benetos [Reference Ycart and Benetos12]. Our annotations are complementary to their annotations.
The rest of the paper is organized as follows. Section II reviews related work on acoustic and language modeling. Section III explains the unified model based on acoustic and language models, and Section IV describes Bayesian inference of the model parameters and latent variables. Section V reports comparative evaluation using piano music data, and Section VI summarizes the paper.
II. RELATED WORK
This section reviews related work on acoustic modeling, language modeling, and integrated acoustic and language modeling for AMT.
A) Acoustic modeling
NMF and probabilistic latent component analysis (PLCA) are conventionally applied as the methods for spectrogram decomposition [Reference Smaragdis and Brown1–Reference Vincent, Bertin and Badeau4,Reference Liang and Hoffman9,Reference Cemgil13–Reference Benetos and Weyde18]. NMF approximates a non-negative matrix (a magnitude spectrogram) as the product of two non-negative matrices; bases (a set of spectral templates corresponding to different pitches or timbres) and activations (a set of gain vectors). Similarly, PLCA approximates a normalized spectrogram as a bivariate probability distribution and decomposes it into a series of spectral templates, pitches, instruments, and so on.
Smaragdis [Reference Smaragdis19] proposed convolutive NMF that uses a time-frequency segment as a template. Virtanen et al. [Reference Virtanen and Klapuri3] reformulated bases as the product of sources corresponding to pitches and filters corresponding to timbres. This extension contributes to reducing the number of parameters and makes the estimation of bases more reliable, especially when different instruments play the same pitch. Vincent et al. [Reference Vincent, Bertin and Badeau4] also extended NMF by forcing each basis to have harmonicity and spectral smoothness. Each pitch is represented as the sum of corresponding bases so that it adaptively fits the spectral envelope of a musical instrument in the observed music signal. O'Hanlon et al. [Reference O'Hanlon and Plumbley20] proposed group-sparse NMF that can represent the co-activity of bases. Using group sparsity in addition to narrow bands proposed in [Reference Vincent, Bertin and Badeau4], they let bases fit more adaptively to the observed signals. Cheng et al. [Reference Cheng, Mauch, Benetos and Dixon15] proposed an attack and decay model for piano transcription.
There have been some attempts to introduce prior knowledge into the NMF framework. Cemgil et al. [Reference Cemgil13] described Bayesian inference for NMF. Hoffman et al. [Reference Hoffman, Blei and Cook2] introduced a Bayesian non-parametric model called γ-process NMF to estimate an appropriate number of bases that are necessary to reconstruct the observation. Liang et al. [Reference Liang and Hoffman9] also proposed a Bayesian non-parametric extension called β-process NMF that multiplies a binary matrix (mask) to the activation matrix.
Deep learning techniques have recently been used for AMT. Nam et al. [Reference Nam, Ngiam, Lee and Slaney21] used a deep belief network for learning latent representations of magnitude spectra and used support vector machines for judging the existence of each pitch. Boulanger-Lewandowski et al. [Reference Boulanger-Lewandowski, Bengio and Vincent22] proposed a recurrent extension of the restricted Boltzmann machine and found that musically plausible transcriptions were obtained.
B) Language modeling
Some studies have attempted to computationally represent music theory. Hamanaka et al. [Reference Hamanaka, Hirata and Tojo23] reformalized a systematized music theory called the generative theory of tonal music (GTTM) [Reference Jackendoff and Lerdahl24] and developed a method for estimating a tree that represents the structure of music called a time-span tree. Nakamura et al. [Reference Nakamura, Hamanaka, Hirata and Yoshii25] also reformalized the GTTM as a probabilistic context-free grammar. These methods enable automatic music parsing. Induction of harmony in an unsupervised manner has also been studied. Hu et al. [Reference Hu and Saul26] used latent Dirichlet allocation to determine the key of a musical piece from symbolic and audio music data based on the fact that the likelihood of the appearance of each note tends to be similar among musical pieces in the same key. This method enables the distribution of pitches in a certain key (key profile) to be obtained without using labeled training data.
Statistical methods of supervised chord recognition [Reference Rocher, Robine, Hanna and Strandh5–Reference Ueda, Uchiyama, Nishimoto, Ono and Sagayama8] are worth investigation for unsupervised music grammar induction. Rocher et al. [Reference Rocher, Robine, Hanna and Strandh5] attempted chord recognition from symbolic music by constructing a directed graph of possible chords and then calculating the optimal path. Sheh et al. [Reference Sheh and Ellis6] used acoustic features called chroma vectors to estimate chords from music signals. They constructed an HMM whose latent variables are chord labels and whose observations are chroma vectors. Maruo et al. [Reference Maruo, Yoshii, Itoyama, Mauch and Goto7] proposed a method that uses NMF for extracting reliable chroma features. Since these methods require labeled training data, the concept of chords is required in advance.
C) Acoustic and language modeling
Multipitch estimation considering both acoustic features and music grammar has recently been studied. Raczyński et al. [Reference Raczyński, Vincent, Bimbot and Sagayama27,Reference Raczyński, Vincent and Sagayama28] proposed a probabilistic pitch model based on a dynamic Bayesian network consisting of several sub-models, each of which describes a different property of pitches. This model in combination with an NMF-based acoustic model performs better in multipitch estimation. Böck et al. [Reference Böck and Schedl29] proposed a method for note onset transcription based on a recurrent neural network (RNN) with long short-term memory (LSTM) units that takes acoustic features as input and outputs a piano roll. Sigtia et al. [Reference Sigtia, Benetos and Dixon30] used an RNN as a language model. They integrated the RNN with a PLCA-based acoustic model so that the output of the RNN is treated as a prior for pitch activations. Holzapfel et al. [Reference Holzapfel and Benetos31] proposed a method that uses tatum information for multipitch estimation. Ycart et al. [Reference Ycart and Benetos32] used an LSTM network that takes a piano roll as an input and predict the next frame. The network is used for the post-processing of the piano roll estimated with the acoustic model proposed in [Reference Benetos and Weyde16]. In their study, tatum information was used to evaluate the note-prediction accuracy.
III. GENERATIVE MODELING
This section explains a generative model of a music spectrogram for estimating pitches and their typical cooccurrences (chords) from music signals. Our model consists of acoustic and language models connected through a piano roll, i.e., a set of binary variables indicating the existences of pitches (Fig. 1). The acoustic model represents the generative process of a music spectrogram from the basis spectra and temporal activations of individual pitches. The language model represents the generative process of chord progressions and pitch locations from chords.
A) Problem specification
The goal of this study is to estimate a piano roll from a music signal played by pitched instruments. Let 
${\bi X} = \{X_{ft}\}_{f,t=1}^{F,T}$ be the log-frequency magnitude spectrogram (e.g., constant-Q transform) of a music signal, where F is the number of frequency bins and T is the number of time frames. Let 
${\bi S} = \{S_{kn}\}_{k,n=1}^{K,N}$ be a piano roll, where 
$S_{kn} \in \{0, 1\}$ indicates the existence of pitch k at the n-th time unit (tatum time or time frame) and K is the number of unique pitches. When we formulate a frame-level model without using tatum information, T=N holds. When we formulate a tatum-level model. the tatum times are assumed to be given or estimated in advance. In addition, we aim to estimate a sequence of chords 
${\bi Z} = \{z_{n}\}_{n=1}^{N}$ over N time units, where 
$z_{n} \in \{1, \ldots, I\}$ indicates a chord at the n-th time unit and I is the number of unique chords.
B) Acoustic modeling
We design a generative model of X inspired by a Bayesian extension of NMF with binary variables [Reference Liang and Hoffman9] (Fig. 2). The spectrogram 
${\bi X} \in {\open R}_+^{F \times T}$ is factorized into basis spectra 
${\bi W} = \{{\bi W}^{h} \in {\open R}_+^{K \times F}, {\bi W}^{n} \in {\open R}_+^{1 \times F}\}$ consisting of K harmonic spectra Wh and a noise spectrum Wn, the corresponding temporal activations 
${\bi H} = \{{\bi H}^{h} \in {\open R}_+^{K \times T}, {\bi H}^{n} \in {\open R}_+^{1 \times T}\}$, and binary variables 
${{\bi S}} \in \{0,1\}^{K \times N}$ as follows:
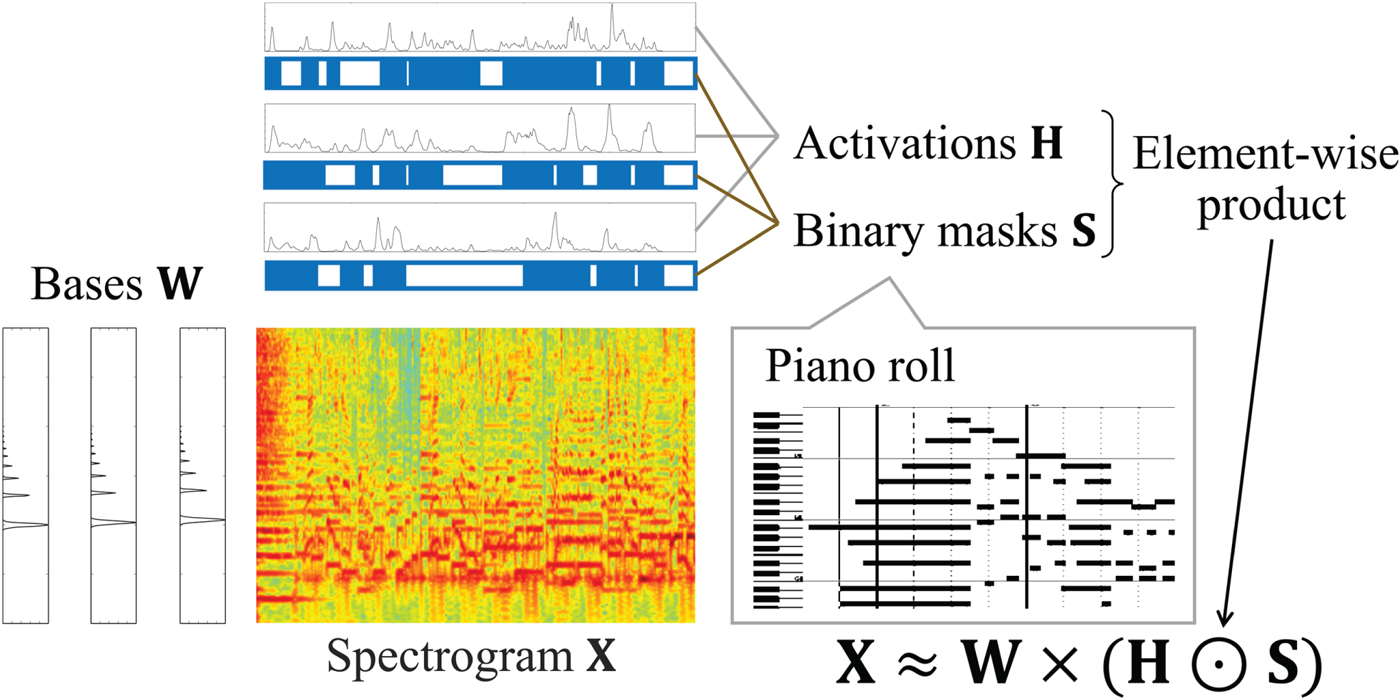
Fig. 2. An acoustic model based on a variant of NMF with binary variables indicating a piano roll.
$$\eqalign{& X_{ft} \vert {\bi W}, {\bi H}, {\bi S} \cr &\quad \sim {\cal P}\!\left(X_{ft} \left\vert \sum_{k=1}^{K}{W^h_{kf} H^h_{kt} S_{kn_t}} + W^n_f H^n_t \right. \right),}$$
where 
${\cal P}$ indicates a Poisson distribution, 
$W_{kf}^{h}$ is the magnitude of harmonic basis k at frequency f, 
$H_{kt}^{h}$ is its gain at frame t, and 
$S_{kn_{t}}$ is a binary variable indicating whether basis k is activated at time n t. Here, n t is a time unit to which frame t belongs to (n t=t in a frame-level model). Similarly, 
$W_{f}^{n}$ and 
$H_{t}^{n}$ are defined for the noise component.
As proposed in [Reference Smaragdis, Raj and Shashanka33], we assume that the harmonic structures of different pitches have shift-invariant relationships as follows:
$$W^h_{kf} = \overline{W}^h_{f_k} \,(1 \le k \le K),$$
where 
$\{\overline{W}^{h}_{f}\}_{f=1}^{F}$ is a template pattern shared by the K harmonic spectra, 
$f_{k} = f - (k - 1) \Delta$ is a shifting interval, and Δ is the number of log-frequency bins corresponding to a semitone. If f k≤0, 
$W^{h}_{kf} = 0$. Although equation (2) is an excessively simplified model of real instrument sounds and the expressive capability of the acoustic model is limited, it contributes to automatically learning a harmonic template without explicitly imposing harmonic constraints (Fig. 3). We put a γ prior on 
$\overline{W}^{h}_{f}$ as follows:
$$\overline{W}^h_f \sim {\cal G}\!\lpar a^h, b^h\rpar ,$$where a h and b h are shape and rate hyperparameters.
As proposed in [Reference Cemgil and Dikmen34], we put a γ chain prior on 
$W^{n}_{f}$ to induce the spectral smoothness as follows:
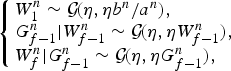$$\left\{\matrix{W^n_{1} \sim {\cal G}\!\lpar \eta, \eta b^n / a^n \rpar , \hfill \cr G^n_{f-1} \vert W^n_{f-1} \sim {\cal G}\!\lpar \eta, \eta W^n_{f-1}\rpar , \hfill \cr W^n_f \vert G^n_{f-1} \sim {\cal G}\!\lpar \eta, \eta G^n_{f-1} \rpar , \hfill}\right.$$
where η is a hyperparameter adjusting the degree of smoothness and 
$G^{n}_{f}$ is an auxiliary variable forcing 
$W^{n}_{f-1}$ to be positively correlated with 
$W^{n}_{f}$. Since 
${\open E}_{prior}[G^{n}_{f-1}] = 1 / W^{n}_{f-1}$ and 
${\open E}_{prior}[W^{n}_{f}] = 1 / G^{n}_{f-1}$, we can roughly say 
${\open E}_{prior}[W^{n}_{f}] \approx {\open E}_{prior}[W^{n}_{f-1}]$ (Fig. 3).
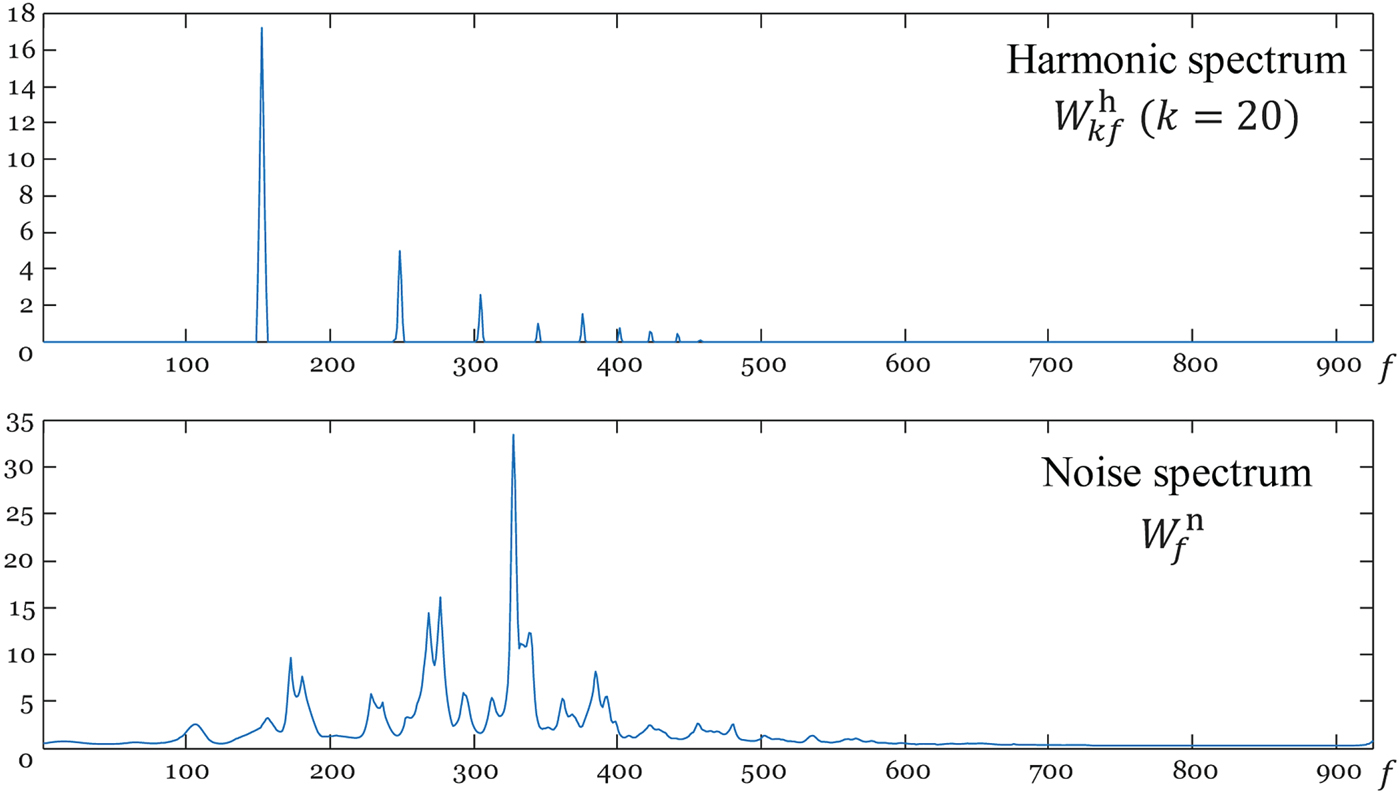
Fig. 3. Harmonic and noise spectra learned from data.
We put γ priors on the activations H as follows:
$$H^h_{kt} \sim {\cal G} \lpar c^h, d^h\rpar ,$$
$$H^n_{t} \sim {\cal G} \lpar c^n, d^n\rpar ,$$where c h, c n, d h, and d n are hyperparameters.
C) Language modeling
We propose an HMM that has latent variables (chords) Z and emits binary variables (pitches) S, which cannot be observed in reality, as follows (Fig. 4):
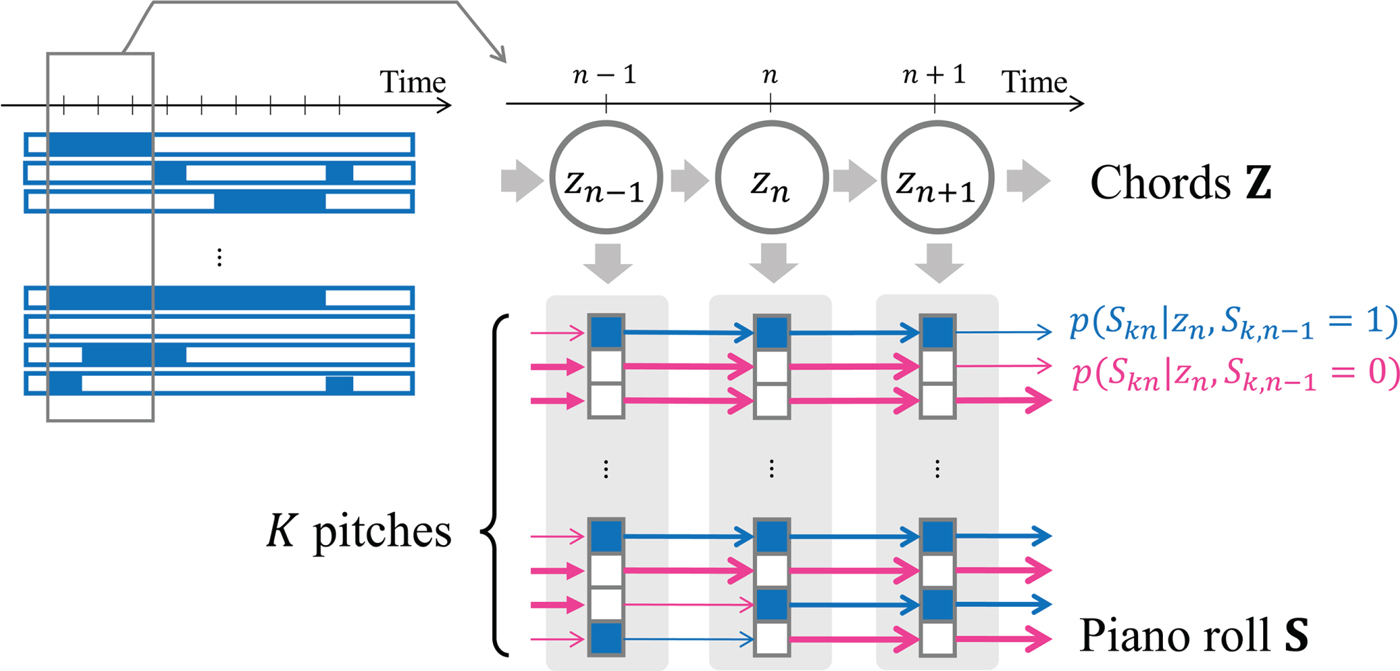
Fig. 4. A language model based on an autoregressive HMM that emits sequentially dependent binary variables.
$$z_1 \vert {\bi \phi} \sim {Categorical}({\bi \phi}),$$
$$z_n \vert z_{n-1}, {\bi \psi} \sim {Categorical}({\bi \psi}_{z_{n-1}}),$$
$$S_{kn} \vert z_n, {\bi \pi} \sim {Bernoulli}(\pi_{z_n,k}),$$
where 
${\bi \phi} \in {\open R}_+^{I}$ is a set of initial probabilities, 
${\bi \psi}_{i} \in {\open R}_+^{I}$ is a set of transition probabilities from chord i, and πik indicates the emission probability of pitch k from chord i. In this paper, we focus on only the emission probabilities of the 12 pitch classes (C, C♯, …, B, m=0, …, 11), which are copied to all octaves covering the K pitches. Let 
$\overline\pi_{jm}$ be the emission probability of pitch class m from chord type j (major or minor, j=0, 1). The emission probabilities from chords of the same type are assumed to have circular-shifting relationships as follows:
$$\pi_{ik} = \overline\pi_{{type}(i), {mod}({class}(k) - {root}(i), 12)},$$
where 
${type}(i) \in \{0,1\}$ and 
${root}(i) \in \{0,\ldots,11\}$ are the type and root note of chord i, respectively, and 
${class}(k) \in \{0,\ldots,11\}$ is the pitch class of pitch k. We put conjugate priors on those parameters as follows:
$${\bi \phi} \sim{Dir}({\bi u}),$$
$${\bi \psi}_i \sim {Dir}({\bi v}_i),$$
$$\overline\pi_{jm} \sim {\beta}(e, f),$$
where 
${\bi u} \in {\open R}_+^{I}$, 
${\bi v}_{i} \in {\open R}_+^{I}$, e, and f are hyperparameters.
This HMM can be extended in an autoregressive manner by incorporating the sequential dependency (smoothness) of binary variables of each pitch. More specifically, equation (9) can be extended as follows [Reference Benetos and Dixon35]:
$$S_{kn} \vert z_n, S_{k,n-1}, {\bi \pi} \sim {Bernoulli}\lpar \pi^{(S_{k,n-1})}_{z_n,k}\rpar ,$$
where 
$\pi^{(S_{k,n-1})}_{z_{n},k}$ indicates the emission probability of pitch k from chord z n at time unit n when the same pitch k is activated (S k, n−1=1) or not activated (S k, n−1=0) at the previous time unit n−1. Instead of equation (13), we consider two types of emission probabilities as follows:
$$\overline\pi^{(0)}_{jm} \sim {\beta}(e^{(0)}, f^{(0)}),$$
$$\overline\pi^{(1)}_{jm} \sim {\beta}(e^{(1)}, f^{(1)}),$$
where 
$e^{(0)}, f^{(0)}, e^{(1)}$, and f (1) are hyperparameters. The circular-shifting relationships between 
$\pi_{ik}^{(0)}$ and 
$\overline\pi^{(0)}_{jm}$ and that between 
$\pi_{ik}^{(1)}$ and 
$\overline\pi^{(1)}_{jm}$ are defined in the same way as equation (10). The self-transitions (i.e., 
$S_{k,n-1} = S_{k,n} = 0$ and 
$S_{k,n-1} = S_{k,n} = 1$) are more likely to occur when 
$e^{(0)} \gg f^{(0)}$ and 
$e^{(1)} \ll f^{(1)}$. This contributes to reducing spurious musical notes that tend to have very short durations. We evaluated the standard HMM given by equations (9) and (13) and the autoregressive HMM given by equations (14)–(16) in Section V.
IV. POSTERIOR INFERENCE
This section describes AMT for the observed data X. We explain Bayesian inference of the proposed model and then describe how to put emphasis on the language model. In addition, we describe how to pre-train the language model.
A) Bayesian inference
Given the observation X, we aim to calculate the posterior distribution 
$p({\bi W},{\bi H},{\bi Z},{\bi S},\brTheta \vert {\bi X})$, where 
$\brTheta = \{{\bi \phi},{\bi \psi},{\bi \pi}\}$. We use Gibbs sampling to approximate the analytically intractable posterior distribution (Algorithm 1). The piano roll S is estimated by using the current acoustic and language models, which are then updated independently by using the current S. These steps are iterated until approximate convergence. Finally, a sequence of chords Z is estimated using the Viterbi algorithm and then S is determined using the maximum-likelihood parameters of the unified model.
Algorithm 1 Posterior inference
1) Updating piano roll
The piano roll S is sampled in an element-wise manner from a conditional posterior distribution (Bernoulli distribution) obtained by integrating the acoustic model with the language model as follows:
$$\eqalign{& p(S_{kn} \vert {\bi X}, {\bi W}, {\bi H}, {\bi Z}, {\bi S}_{\neg kn}, {\brTheta}) \cr &\quad \propto p({\bi X} \vert {\bi W}, {\bi H}, {\bi S}) p(S_{kn} \vert z_n, {\bi S}_{\neg kn}, {\bi \pi}),}$$
where a notation 
$\brOmega_{\neg i}$ indicates a set of all elements of Ω except for the i-th element, the first term (likelihood, acoustic model) is given by equation (1), and the second term (prior, language model) is given by equation (14) as follows:
$$\eqalign{& p(S_{kn} \vert z_n, {\bi S}_{\neg kn}, {\bi \pi})\cr &\quad \propto \lpar \pi_{z_n,k}^{(S_{k,n-1})}\rpar ^{S_{kn}} \lpar 1 - \pi_{z_n,k}^{(S_{k,n-1})}\rpar ^{1 - S_{kn}} \cr &\qquad \times\lpar \pi_{z_{n+1},k}^{(S_{k,n})}\rpar ^{S_{k,{n+1}}} \lpar 1 - \pi_{z_{n+1},k}^{(S_{k,n})}\rpar ^{1 - S_{k,{n+1}}}.}$$When the sequential dependency of S is not considered, equation (18) is simplified as follows:
$$p(S_{kn} \vert z_n, {\bi S}_{\neg kn}, {\bi \pi}) \propto \lpar \pi_{z_n,k}\rpar ^{S_{kn}} \lpar 1 - \pi_{z_n,k}\rpar ^{1 - S_{kn}}.$$2) Updating acoustic model
The parameters W and H of the acoustic model are sampled using Gibbs sampling in the same way as [Reference Liang and Hoffman9]. Note that Wh and H have γ priors and Wn have γ chain priors. Because of the conjugacy, we can easily calculate the γ posterior of each variable conditioned on the other variables and the binary variables.
Using the Bayes’ rule, the conditional posterior distribution of 
$\overline{{\bi W}}^{h}$ is given by
$$p(\overline{{\bi W}}^h \vert {\bi X}, {\bi W}^n, {\bi H}, {\bi Z}, {\bi S}) \propto p({\bi X} \vert {\bi W}, {\bi H}, {\bi S}) p(\overline{{\bi W}}^h),$$where the first term (likelihood) is given by equation (1) and the second term (prior) is given by equation (3). More specifically, we obtain
$$\eqalign{\overline{W}^h_f &\sim {\cal G}\! \left(\sum_{k=1}^K \sum_{t=1}^T X_{\tilde{f}_kt} \lambda_{\tilde{f}_ktk}^h + a^h,\right. \cr & \left.\sum_{k=1}^K \sum_{t=1}^T H_{kt}^h S_{kn_t} + b^h\right),}$$
where 
$\tilde{f}_{k} = f + (k-1)\Delta$ (if f̃ k>F, 
$X_{\tilde{f}_{k}t}=0$) and 
$\lambda_{ftk}^{h}$ is an auxiliary variable obtained by using the previous samples of W, H, and S as follows:
$$\lambda^h_{ftk} = \displaystyle{W^h_{kf} H^h_{kt} S_{k n_t} \over \sum_{k'} W^h_{k'f} H^h_{k't} S_{k' n_t} + W^n_f H^n_t}.$$Since Wn and Gn are interdependent in equation (4), Wn and Gn are sampled alternately as follows:
$$\eqalign{& p({\bi W}^n \vert {\bi X}, {\bi W}^h, {\bi G}^n, {\bi H}, {\bi Z}, {\bi S}) \cr &\quad \propto p({\bi X} \vert {\bi W}, {\bi H}, {\bi S}) p({\bi W}^n, {\bi G}^n),}$$
$$p({\bi G}^n \vert {\bi X}, {\bi W}^h, {\bi W}^n, {\bi H}, {\bi Z}, {\bi S}) \propto p({\bi W}^n, {\bi G}^n),$$where the first and second terms of equation (23) are given by equations (1) and (4), respectively. More specifically, we obtain
$$\eqalign{W^n_f &\sim {\cal G}\! \left(\sum_{t=1}^T X_{ft} \lambda^n_{ft} + \eta,\right. \cr &\qquad \left.\sum_{t=1}^T H^n_t + \eta \lpar G^n_{f+1} + G^n_f\rpar \right),}$$
$$G^n_f \sim {\cal G}\! \lpar \eta, \eta\lpar W^n_f + W^n_{f-1}\rpar \rpar ,$$
where 
$\lambda_{ft}^{n}$ is an auxiliary variable given by
$$\lambda^n_{ft} = \displaystyle{W^n_f H^n_t \over \sum_{k'} W^h_{k'f} H^h_{k't} S_{k' n_t} + W^n_f H^n_t}.$$The conditional posterior distribution of H is given by
$$p({\bi H} \vert {\bi X}, {\bi W}, {\bi Z}, {\bi S}, \brTheta) \propto p({\bi X} \vert {\bi W}, {\bi H}, {\bi S}) p({\bi H}),$$where the first term (likelihood) is given by equation (1) and the second term (prior) is given by equations (3) and (6). More specifically, we obtain
$$H^h_{kt} \sim {\cal G} \left(\sum_{f=1}^F X_{ft} \lambda_{ftk}^h + c^h, \ S_{kn_t} \sum_{f=1}^F W^h_{kf} + d^h\!\right),$$
$$H^n_t \sim {\cal G}\! \left(\sum_{f=1}^F X_{ft} \lambda_{ft}^n + c^n, \sum_{f=1}^F W^n_f + d^n\right).$$3) Updating chord sequence
The latent variables Z can be updated efficiently by using a forward filtering-backward sampling algorithm, which is a stochastic version of the forward-backward algorithm (Baum–Welch algorithm). The conditional posterior distribution of Z is given by
$$p({\bi Z} \vert {\bi S}, {\brTheta}) \propto p({\bi S} \vert {\bi Z}, {\bi \pi}) p({\bi Z} \vert {\bi \phi}, {\bi \psi}),$$
where the first term is given by equation (9) and the second term is given by equations (7) and (8). Let a Matlab-like notation s1:n denote 
$\{{\bi s}_{1}, \ldots, {\bi s}_{n}\}$, where 
${\bi s}_{n} = [S_{n1},\ldots,S_{nK}]^{T}$. Henceforth, we often omit the dependency on Θ for brevity (Θ is assumed to be given for estimating Z). As in a standard HMM, a forward message 
$\alpha(z_{n}) = p({\bi s}_{1:n}, z_{n})$ can be calculated recursively as follows:
$$\alpha(z_1) = p(z_1) p({\bi s}_1 \vert z_1),$$
$$\alpha(z_n) = p({\bi s}_n \vert z_n, {\bi s}_{n-1}) \sum_{z_{n-1}} p(z_n \vert z_{n-1}) \alpha(z_{n-1}),$$
where 
$p(z_{1}) = \phi_{z_{1}}$, 
$p(z_{n} \vert z_{n-1}) = \psi_{z_{n-1}, z_{n}}$, and 
$p({\bi s}_{1} \vert z_{1})$ and 
$p({\bi s}_{n} \vert z_{n}, {\bi s}_{n-1})$ are given by equation (14) or equation (9).
After calculating the forward messages, we perform the backward sampling as follows:
$$p({\bi Z} \vert {\bi S}) = p(z_N \vert {\bi S}) \prod_{n=1}^{N-1} p(z_n \vert {\bi S}, z_{n+1:N}),$$More specifically, the last latent variable z N is sampled as follows:
$$z_N \sim p(z_N \vert {\bi S}) \propto \alpha(z_N).$$The other latent variables z 1:N−1 are then sampled recursively in the reverse order as follows:
$$z_n \sim p(z_n \vert {\bi S}, z_{n+1:N}) \propto p(z_{n+1} \vert z_n) \alpha(z_n).$$4) Updating language model
Using the Bayes’ rule, the posterior distribution of the emission probabilities 
$\overline{{\bi \pi}}$ is given by
$$p(\overline{{\bi \pi}} \vert {\bi S}, {\bi Z}) \propto p({\bi S} \vert {\bi Z}, \overline{{\bi \pi}}) p(\overline{{\bi \pi}}),$$where the first term (likelihood) is given by equation (9) and the second term (prior) is give by equation (15) and equation (16). More specifically, we obtain
$$\overline{\pi}^{(0)}_{jm} \sim {\beta}\! \lpar e^{(0)}+r^{(01)}_{jm}, f^{(0)}+r^{(00)}_{jm}\rpar ,$$
$$\overline{\pi}^{(1)}_{jm} \sim {\beta} \!\lpar e^{(1)}+r^{(11)}_{jm}, f^{(1)}+r^{(10)}_{jm}\rpar ,$$
where 
$r^{(00)}_{jm}$, 
$r^{(01)}_{jm}$, 
$r^{(10)}_{jm}$, and 
$r^{(11)}_{jm}$ are count data given by
$$r^{(00)}_{jm} = \sum_{n \in A_j} \sum_{k \in B_{nm}} (1 - S_{k,n-1}) (1 - S_{kn}),$$
$$r^{(01)}_{jm} = \sum_{n \in A_j} \sum_{k \in B_{nm}} (1 - S_{k,n-1}) S_{kn},$$
$$r^{(10)}_{jm} = \sum_{n \in A_j} \sum_{k \in B_{nm}} S_{k,n-1} (1 - S_{kn}),$$
$$r^{(11)}_{jm} = \sum_{n \in A_j} \sum_{k \in B_{nm}} S_{k,n-1} S_{kn},$$
where A j and B nm are subsets of indices given by 
$A_{j} = \{n \vert {type}(z_{n}) = j\}$ and 
$B_{nm} = \{k \vert {mod}({class}(k) - {root}(z_{n}),\break 12) = m\}$. When the sequential dependency of S is not considered, we obtain
$$\overline{\pi}_{jm} \sim {\beta}\! \lpar e + r^{(00)}_{jm} + r^{(10)}_{jm}, f + r^{(01)}_{jm} + r^{(11)}_{jm}\rpar .$$The posterior distributions of the initial probabilities ϕ and the transition probabilities ψ are given by
$$p({\bi \phi}, {\bi \psi} \vert {\bi S}, {\bi Z}) \propto p({\bi Z} \vert {\bi \phi}, {\bi \psi}) p({\bi \phi}) p({\bi \psi}),$$where the first term is given by equations (7) and (8), the second term is given by equation (11), and the third term is given by equation (12). More specifically, we obtain
$${\bi \phi} \sim {Dir}\lpar {\bf 1}_I + {\bi e}_{z_1}\rpar ,$$
$${\bi \psi}_i \sim {Dir} \lpar {\bi v}_i + {\bi u}_i\rpar ,$$where ei is the unit vector whose i-th element is 1 and ui is the I-dimensional vector whose j-th element indicates the number of transitions from state i to state j.
B) Weighted integration
In naive integration of the language model and acoustic models, the language model does not effectively affect the posterior distribution of piano roll S, i.e., musically inappropriate allocation of musical notes is not given a large penalty. To balance the impact of the language model with that of the acoustic model, we introduce a weighting factor α as in ASR, i.e., equation (18) is replaced with
$$\eqalign{& p(S_{kn} \vert z_n, {\bi S}_{\neg kn}, {\bi \pi}) \cr &\quad \propto \lpar \lpar \pi_{z_n,k}^{(S_{k,n-1})}\rpar^{S_{kn}} \lpar 1 - \pi_{z_n,k}^{(S_{k,n-1})}\rpar^{1 - S_{kn}} \cr &\qquad \times \lpar \pi_{z_{n+1},k}^{(S_{k,n})}\rpar^{S_{k,{n+1}}} \lpar 1 - \pi_{z_{n+1},k}^{(S_{k,n})}\rpar^{1 - S_{k,{n+1}}} \rpar ^{\alpha D_n},}$$where D n indicates the number of time frames in time unit n. When the sequential dependency of S is not considered, equation (19) is replaced with
$$\eqalign{& p(S_{kn} \vert z_n, {\bi S}_{\neg kn}, {\bi \pi}) \cr &\quad \propto \lpar \lpar \pi_{z_n,k}\rpar^{S_{kn}} \lpar 1 - \pi_{z_n,k}\rpar^{1 - S_{kn}} \rpar ^{\alpha D_n}.}$$We empirically investigated the effect of these modifications (see Section V).
C) Prior training
The language model can be trained in advance from existing piano rolls (musical scores) even if no chord annotations are available. Here we assume that there a single piano roll Ŝ is given as training data for simplicity because it is straightforward to deal with multiple piano rolls. The underlying chords Ẑ and the parameters 
$\brTheta = \{{\bi \phi},{\bi \psi},{\bi \pi}\}$ can be estimated from Ŝ instead of S as in Section IV-A-3. After using the Gibbs sampling, we determine Ẑ by using the Viterbi algorithm and calculate the posterior distributions of 
$\overline{{\bi \pi}}$ based on the estimate of Ẑ according to equations (38) and (39), which is then used as a prior distribution of 
$\overline{{\bi \pi}}$ instead of equations (15) and (16). This is a strong advantage of Bayesian formulation. Since the chord transitions are different for each musical piece, ϕ and ψ are trained in an unsupervised manner.
V. EVALUATION
We evaluated the performance of the proposed method for AMT. First, we conducted a preliminary experiment to confirm that the language model can learn chord progressions and typical cooccurrences of pitches from piano rolls in an unsupervised manner. Next, we evaluated the performances of multipitch estimation obtained by using different language models and those obtained by the pre-trained and unsupervised models. Finally, we compared the proposed model with several unsupervised models.
A) Experimental conditions
We used 30 classical piano pieces labeled as ‘ENSTDkCl’ selected from the MAPS database [Reference Emiya, Badeau and David11]. An audio signal of 30 sec was extracted from the beginning of each piece. The magnitude spectrogram of size F=926 and T=3000 was obtained using variable-Q transform [Reference Schörkhuber, Klapuri, Holighaus and Dörfler36], where the number of frequency bins in one octave was set to 96. A harmonic and percussive source separation method [Reference Fitzgerald37] was used for suppressing non-harmonic components. All hyperparameters were determined empirically for maximizing the performance as described below.
We considered K=84 unique pitches (MIDI note numbers 21–104) and I=24 unique chords. We manually made tatum and chord annotations on 16th-note-level grids.Footnote 1 Since noise components were assumed to be smaller than harmonic components, the hyperparameters of Wh and Wn were set as a h=b h=1, a n=2, and b n=4 such that 
${\open E}[\overline{W}^{h}_{f}] = 1$ and 
${\open E}[W^{n}_{f}] = 0.5$. The hyperparameters of Hh were set as c h=10 and d h=10 to favor non-zero gains. This was effective to avoid 
$S_{k n_{t}} = 1$ when H kt takes almost zero. The hyperparameters of Hn, on the other hand, were set as c n=5 and d n=5 to allow 
$H^{n}_{t}$ to take almost zero. The hyperparameters of π were set as 
$e = e^{(1)} = e^{(0)} = 10^{-9}, f = f^{(1)} = f^{(0)} = 1$ to make a binary matrix S sparse. The hyperparameter η was empirically determined as η=30000.
We tested two kinds of time resolutions for the language model, i.e., a frame-level model with a time resolution of 10 ms and a tatum-level model defined on a 16th-note-level grid. The hyperparameter of the initial probabilities ϕ was set as 
${\bi u}=[1,\ldots,1]^{\rm T} \in {\open R}^{I}$. In the frame-level model, the self-transition probability of each chord i was set as 
$\psi_{ii}=0.99$ to favor temporal continuity and the transition probabilities from chord i to the other 23 chords were assumed to follow a Dirichlet distribution, 
$100 {\bi \psi}_{i,\neg i} \sim {Dir}({\bf 1}_{I-1})$. In the tatum-level model, the hyperparameter of the transition probabilities ψ was set as 
${\bi v}_{i} = [0.2, \ldots, 1, \ldots, 0.2]^{\rm T} \in {\open R}^{I}$, where only the i-th dimension takes 1. The weighting factor of the language model, which has a strong impact on the performance, was empirically set to α=12.5 unless otherwise noted.
B) Chord estimation for piano rolls
We investigated whether chord progressions and typical cooccurrences of pitches (chords) can be learned from a piano roll obtained by concatenating the ground-truth piano rolls of the 30 pieces. The size of the matrix used as an input was thus 
$84 \times \sum_{i=1}^{30} N_{i}$, where N i indicates the number of time frames or tatum times in the beginning 30 s of the i-th musical piece. We measured the performance of chord estimation as the ratio of the number of correctly estimated time frames or tatum times to the total number of those with major, minor, dominant 7th, and minor 7th chords. Dominant 7th was treated as a major chord, minor 7th as a minor chord, and the other chords were ignored. Since chords were estimated in an unsupervised manner, the estimated states were associated with chord labels to maximize the performance while conserving circular-shifting relationships.
As shown in Table 1, the accuracy of unsupervised chord estimation was around 60% and the tatum-level model outperformed the frame-level model. As shown in Fig. 5, chord structures (emission probabilities 
$\overline{{\bi \pi}}_{0}$ and 
$\overline{{\bi \pi}}_{1}$) corresponding to major and minor chords were learned when all the elements of S were assumed to be independent. When the sequential dependency of S was considered, the emission probabilities 
$\overline{{\bi \pi}}_{0}^{(0)}$, 
$\overline{{\bi \pi}}_{1}^{(0)}$, 
$\overline{{\bi \pi}}_{0}^{(1)}$, and 
$\overline{{\bi \pi}}_{1}^{(1)}$ were strongly affected by the previous binary variables, as shown in Fig. 6. Interestingly, when the previous binary variables were 0, typical pitch structures corresponding to a major chord and the diatonic scale were learned. This implies that a musical scale is more focused on than a chord when a new sound occurs. When the previous binary variable of a pitch was 1, the model prefers to continuously activate the pitch regardless of its pitch class because musical sounds usually continue for several time units.
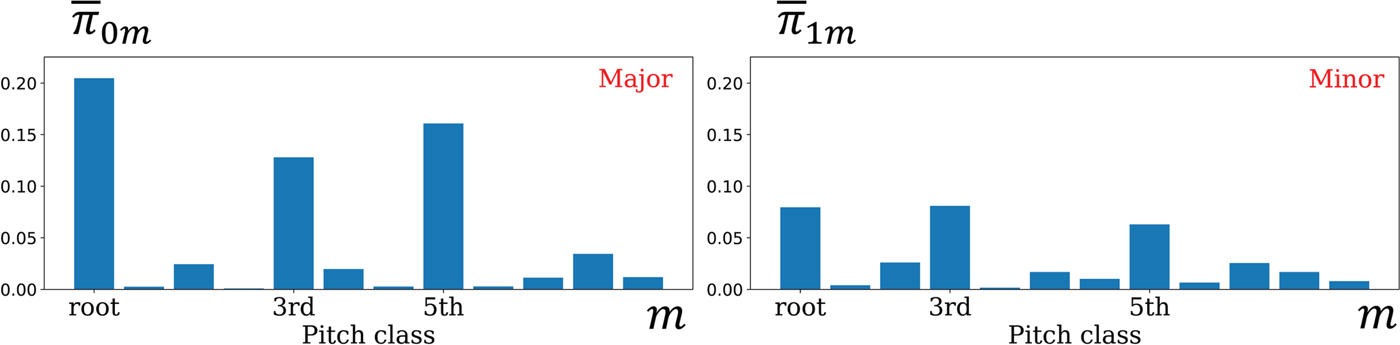
Fig. 5. The emission probabilities 
$\overline{{\bi \pi}}$ obtained by the tatum-level model assuming the independence of S.
Fig. 6. The emission probabilities 
$\overline{{\bi \pi}}$ obtained by the tatum-level model assuming the sequential dependency of S.
Table 1. Accuracy of unsupervised chord estimation.
C) Multipitch estimation for music signals
We evaluated the performance of multipitch estimation in the frame level in terms of the recall rate, precision rate, and F-measure defined as
$$\eqalign{{\cal R} = \displaystyle{\sum_{t=1}^T c_t \over \sum_{t=1}^T r_t}, \quad {\cal P} = \displaystyle{\sum_{t=1}^T c_t \over \sum_{t=1}^T e_t}, \quad {\cal F} = \displaystyle{2{\cal R}{\cal P} \over {\cal R} + {\cal P}},}$$where r t, e t, and c t indicate the numbers of ground-truth, estimated, and correct pitches at time frame t, respectively. The tatum-level measures are defined similarly.
In addition, we measured the note-onset F-measure 
${\cal F}_{on}$ [Reference Dixon38] defined as follows:
$$\eqalign{{\cal R}_{on} = \displaystyle{N_{det} \over N_{gt}},\ {\cal P}_{on} = \displaystyle{N_{cor} \over N_{est}}, {\cal F}_{on} = \displaystyle{2{{\cal R}}_{on}{{\cal P}}_{on} \over {\cal R}_{on} + {{\cal P}}_{on}},}$$where N det is the number of musical notes that were included both in the ground-truth data and in output of the model, N gt is the number of musical notes in the ground-truth data, N cor is the number of musical notes regarded as correct in the estimated notes, and N est is the number of musical notes in the output. For the frame-level model, an estimated note was regarded as correct if its pitch matched a ground-truth pitch and its onset was within 50 ms of the ground-truth onset. A musical note in the ground-truth data was regarded as detected if its pitch matched an estimated pitch and its onset was within 50 ms of an estimated note onset. For the tatum-level model, an estimated note was regarded as correct only if both its pitch and onset matched the ground-truth ones. A musical note in the ground-truth data was regarded as detected if both its pitch and its onset matched the estimated ones.
1) Evaluation of language modeling
We evaluated the effectiveness of each component of the language model by testing different priors on piano roll S. More specifically, we compared the performances of the following five conditions:
(a) Uniform model: The emission probabilities π were fixed to 0.0625.
(b) Sparse model [Reference Liang and Hoffman9]: The emission probabilities π were assumed to be independent and were given sparse prior distributions
$\pi_{ik} \sim {\beta}(10^{-9}, 1)$.(c) Key-aware model: The emission probabilities π were estimated by fixing the latent variables Z to the same value, i.e.,
$z_{1} = \cdots = z_{N} = 1$. In this case, the emission probabilities $\overline{{\bi \pi}}_{1}$ of the 12 pitch classes were expected to indicate the key profile of a target piece.(d) Chord-aware model (HMM): Both Z and π were estimated by equations (36) and (44), respectively, without considering the sequential dependency of each pitch.
(e) Chord-aware Markov model (autoregressive HMM): Both Z and π were estimated by equation (36) and equations (38) and (39), respectively, based on the sequential dependency of each pitch.
We further examined the impact of the weighting factor α by testing α=1 and α=12.5 under the conditions (b) and (d). The performances were measured in the frame or tatum level. To evaluate the frame-level model in the tatum level, the existence of each pitch in each tatum interval was determined by taking the majority of binary variables in the interval. It was straightforward to evaluate the tatum-level model in the frame level.
As shown in Tables 2 and 3, the chord-aware model that does not consider sequential dependency of pitches performed best (69.8% without tatum information and 71.3% with tatum information). Note that the tatum information was not used in the frame-level evaluation of the frame-level model while it was used under the other conditions for estimation and/or evaluation. The F-measure obtained by the frame-level model was improved for 28 out of the 30 pieces (58.8% → 69.8%) by jointly estimating chords and pitches, even when the language and acoustic models were equally considered (56.8 → 57.6%). If the weighting factor α was increased from α=1 to α=12.5, the F-measure was significantly improved from 57.6 to 69.8%, even when the only key profile was learned (69.3%). This indicates the effectiveness of the language model weighting as discussed in Section IV-B. Introducing chord transitions further improved the F-measure from 69.3 to 69.8%.
Table 2. Experimental results of multipitch analysis based on the frame-level model for 30 piano pieces labeled as ENSTDkCl.
Table 3. Experimental results of multipitch analysis based on the tatum-level model for 30 piano pieces labeled as ENSTDkCl.
Examples of estimated piano rolls are shown in Fig. 7. The F-measure obtained by the sparse model (Fig. 7(a)) was improved by 1.7 pts by estimating chords (Fig. 7(b)), and was further improved by 3.1 pts by emphasizing the language model (Fig. 7(c)). The sequential-dependency modeling of a piano roll, however, degraded the performance (Fig. 7(d)). As shown in Fig. 9, the emission probabilities estimated by the chord-aware Markov model indicate that the language model tends to focus on temporal continuity of pitches instead of learning typical note cooccurrences as chords. To solve this problem, the language model should be improved to separately deal with the dependencies of each musical note on the previous note and the current chord.
Fig. 7. Piano rolls estimated for MUS-chpn_p19_ENSTDkCl. (a) Sparse model, (b) chord-aware model (α=1), (c) chord-aware model (α=12.5), (d) chord-aware Markov model (α=12.5).
The similar results were obtained by the tatum-level model. Contrary to expectations, the F-measures obtained by the tatum-level model were not as good as those obtained by the frame-level model in the tatum-level evaluation. The piano rolls estimated by both models are shown in Fig. 8, where the tatum-level model outperformed and underperformed the frame-level model in the upper and lower examples, respectively. The tatum-level model tended to overestimate the durations of musical notes because the acoustic likelihood used for sampling a binary variable S kn is given by the product of the acoustic likelihoods of all time frames contained in tatum unit n. If the likelihood of S kn=1 was larger by several orders of magnitude than that of S kn=0 at a time frame, the acoustic likelihood of the tatum unit tended to support S kn=1. The tatum-level model thus performed worse than the frame-level model, even in the tatum-level evaluation, when musical notes (e.g., triplet or arpeggio) that cannot be represented on a 16th-note-level grid were included in a target piece (Fig. 8). In such cases, the tatum-level model worked well, as shown in the upper example.
Fig. 8. Piano rolls of two musical pieces estimated by using the frame-level and tatum-level models.
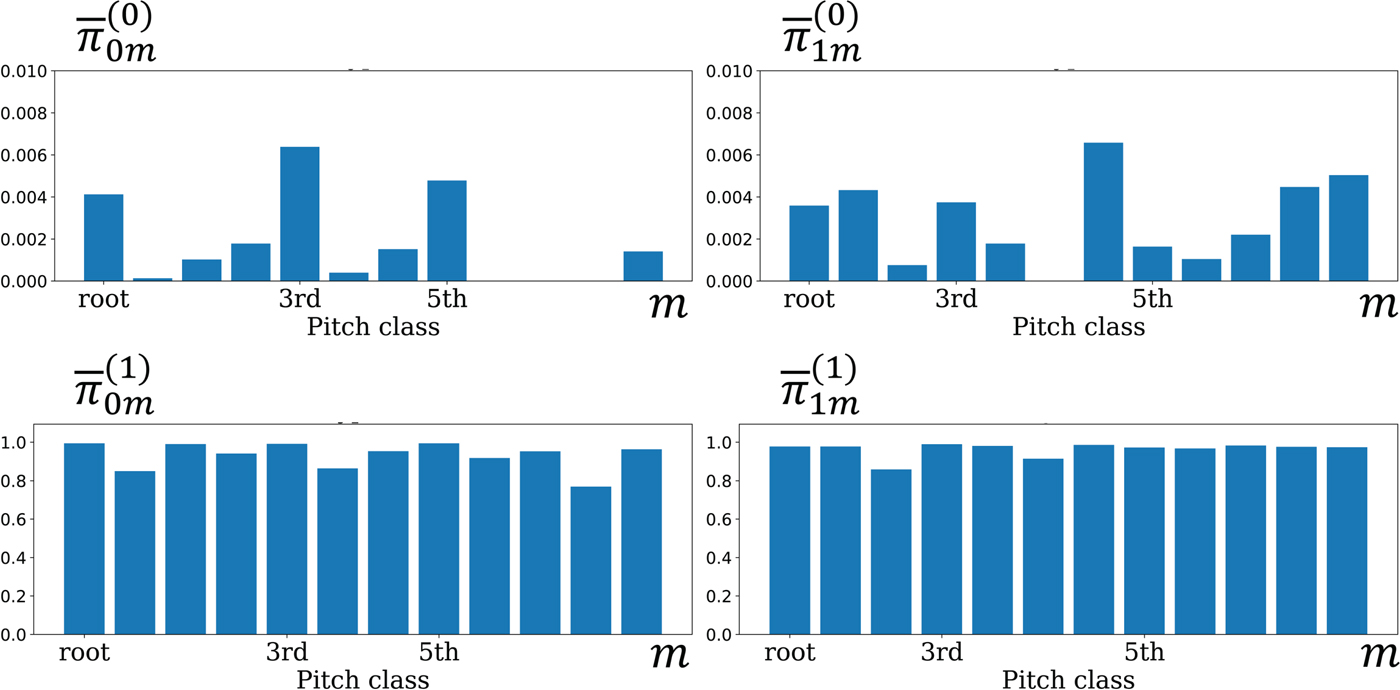
Fig. 9. The emission probabilities 
$\overline{{\bi \pi}}$ estimated for MUS-chpn_p19_ENSTDkCl.
2) Evaluation of prior training
We evaluated the effectiveness of prior training of the language model via leave-one-out cross validation in which one musical piece was used for evaluation and the others were used for training the language model. We compared the performances of the following three conditions:
(a) Baseline: The whole model was trained in an unsupervised manner. This model is the same as the chord-aware model (d) in Section V-C-1.
(b) Learning from piano rolls without chord annotations: The ground-truth piano rolls were used for training the language model while estimating underlying chords.
(c) Learning from piano rolls with chord annotations: The ground-truth piano rolls with ground-truth chord annotations were used for training the language model.
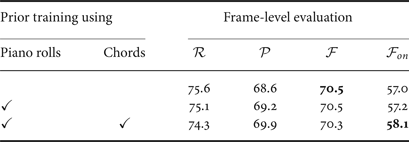
As shown in Tables 4 and 5, the note-onset F-measures were improved by 1.8 pts in the frame-level model and 1.1 pts in the tatum-level model thanks to the improvement of the precision rate when the language model was trained by using piano rolls with chord annotations. We found that musically unnatural short musical notes can be avoided by using the pretrained language model, i.e., considering the note components of chords. On the other hand, the frame-wise F-measures remained almost the same, while the accuracy of chord estimation was improved by 15.0% in the frame-level model and 14.1% in the tatum-level model. One reason for this would be that the musical notes that were wrongly detected by the baseline method and were corrected by the language model were very short and had little impact on the frame-wise F-measures. Another reason is that the typical note cooccurrences could be learned as chords even in an unsupervised condition. We thus need to incorporate other musical structures (e.g., rhythm structures or phrase structures) in the language model.
Table 4. Experimental results of multipitch analysis based on the pre-trained frame-level model.
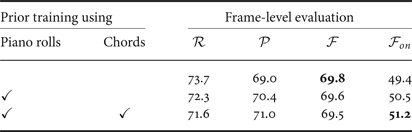
Table 5. Experimental results of multipitch analysis based on the pre-trained tatum-level model.
3) Comparison with existing methods
We compared the performance of the proposed model with four existing unsupervised models: two PLCA-based models proposed by Benetos et al. [Reference Benetos and Weyde16] and by Berg-Kirkpatrick et al. [Reference Berg-Kirkpatrick, Andreas and Klein17] and two NMF-based models proposed by Vincent et al. [Reference Vincent, Bertin and Badeau4] and by O'Hanlon et al. [Reference O'Hanlon and Plumbley20]. These models were trained using audio data produced by pianos that were not included in the test data.
Table 6 shows the performances reported in [Reference Berg-Kirkpatrick, Andreas and Klein17] and obtained by the proposed model. Our model, required no prior training, outperformed the NMF-based method [Reference Benetos and Weyde16] by 1.8 pts in terms of the frame-level F-measure. This considered to be promising because the NMF-based models [Reference Vincent, Bertin and Badeau4,Reference O'Hanlon and Plumbley20] are purely based on acoustic modeling and could be extended in the same way as the proposed model.
Table 6. Performance comparison between five methods.
VI. CONCLUSION
This paper presented a unified statistical model for multipitch analysis that can jointly estimate pitches and chords from music signals in an unsupervised manner. The proposed model consists of an acoustic model (Bayesian NMF) and a language model (Bayesian HMM), and both models can contribute to estimating a piano roll. When a piano roll is given, these models can be updated independently. The piano roll can then be estimated considering the difference in time resolution between the two models.
The experimental results showed the potential of the proposed method for unified music transcription and grammar induction. Although the performance of multipitch estimation was improved by iteratively updating the language and acoustic models, the proposed model did not always outperform other existing methods. The main reason is that simplified acoustic and language models (shift invariance of basis spectra and local dependency of pitches) are used in the current model because the main goal of this paper is to show the effectiveness of integrating the acoustic and language models and the feasibility of unsupervised joint estimation of chords and pitches.
We plan to integrate the state-of-the-art acoustic models such as [Reference O'Hanlon and Plumbley20] and [Reference Cheng, Mauch, Benetos and Dixon15] with our language model. To improve the language model, we need to deal with music grammar of chords, rhythms, and keys. Probabilistic rhythm models, for example, have already been proposed by Nakamura et al. [Reference Nakamura, Yoshii and Sagayama39], which could be integrated with our language model. Moreover, we try to use a deep generative model as a language model to learn more complicated music grammar. Since the performance of the proposed method is considered to be degraded if we use tatum times obtained by a beat tracking method instead of using correct tatum times, joint estimation of tatum times, pitches, and chords is another important direction of research.
Our approach has a deep connection to language acquisition. In the field of natural language processing, unsupervised grammar induction from a sequence of words and unsupervised word segmentation for a sequence of characters have actively been studied [Reference Johnson40,Reference Mochihashi, Yamada and Ueda41]. Since our model can directly infer music grammars (e.g., chord compositions) from either musical scores (discrete symbols) or music signals, the proposed technique is expected to be useful for the emerging topic of language acquisition from continuous speech signals [42].
FINANCIAL SUPPORT
This study was partially supported by JSPS KAKENHI No. 26700020 and No. 16H01744, JSPS Grant-in-Aid for Fellows No. 16J05486, and JST ACCEL No. JPMJAC1602.
Yuta Ojima received the M.S. degree in informatics from Kyoto University, Kyoto, Japan, in 2018. His expertise is automatic music transcription.
Eita Nakamura received the Ph.D. degree in physics from the University of Tokyo, Tokyo, Japan, in 2012. After having been a Postdoctoral Researcher at the National Institute of Informatics, Meiji University, and Kyoto University, Kyoto, Japan, he is currently a Research Fellow of Japan Society for the Promotion of Science. His research interests include music modeling and analysis, music information processing, and statistical machine learning.
Katsutoshi Itoyama received the M.S. and Ph.D. degrees in informatics from Kyoto University, Kyoto, Japan, in 2008 and 2011, respectively. He had been an Assistant Professor at the Graduate School of Informatics, Kyoto University, until 2018 and is currently a Senior Lecturer at Tokyo Institute of Technology. His research interests include musical sound source separation, music listening interfaces, and music information retrieval.
Kazuyoshi Yoshii received the M.S. and Ph.D. degrees in informatics from Kyoto University, Kyoto, Japan, in 2005 and 2008, respectively. He had been a Senior Lecturer and is currently an Associate Professor at the Graduate School of Informatics, Kyoto University, and concurrently the Leader of the Sound Scene Understanding Team, RIKEN Center for Advanced Intelligence Project, Tokyo, Japan. His research interests include music analysis, audio signal processing, and machine learning.
Open access
