This note gives a necessary and sufficient condition that a compressible, isotropic elastic material should admit non-trivial states of finite anti-plane shear.

A method is proposed for the numerical solution of Itô stochastic differential equations by means of a second-order Runge–Kutta iterative scheme rather than the less efficient Euler iterative scheme. It requires the Runge–Kutta iterative scheme to be applied to a different stochastic differential equation obtained by subtraction of a correction term from the given one.

Continental shelf waves are examined for side band instability. It is shown that a modulated shelf wave is described by a nonlinear Schrödinger equation, from which the stability criterion is derived. Long shelf waves are stable to side band modulations, but as the wavenumber is increased there are regions of instability (in wavenumber space). A change of stability occurs at each long wave resonance, defined by the condition that the group velocity of the shelf wave equals a long wave speed. Equations describing the long wave resonance are derived.

Existence of piecewise optimal control is proved when the cost function includes one or both of (a) a cost of sudden switching (discontinuity) of control variables, and (b) a cost associated with the maximum rate of variation of the control over segments of the path for which the control is continuous.

A local description of space and time in which translations are included in the group of gauge transformations is studied using the formalism of fibre bundles. It is shown that the flat Minkowski space–time may be obtained from a non-flat connection in a de Sitter structured fibre bundle by choosing at least two different cross-sections. The interaction terms in the covariant derivative of a Dirac wave function that correspond to translations may be interpreted as the mass term of the Dirac equation, and then the two cross-sections (gauges) correspond to the description of a fermion and antifermion respectively.

A direct numerical computation is provided for the impedance of a screen consisting of a regular array of slits in a plane wall. The problem is solved within the framework of oscillatory Stokes flow, and results presented as a function of porosity, frequency and viscosity.

A detailed analytical and numerical study is made of the deformation of highly elastic circular cylinders and tubes produced by steady rotation about the axis of symmetry. Explicit results are obtained through the use of Ogden's strain–energy function for incompressible isotropic elastic materials which, as well as being analytically convenient, is capable of reproducing accurately the observed isothermal behaviour of vulcanized rubber over a wide range of deformations. The three problems of steady rotation considered here concern (i) a tube shrink-fitted to a rigid spindle, (ii)an unconstrained tube, and (iii) a solid cylinder. In each case a set of restictions on the material constans appearing in the strain–energy function is stated which ensures that a tubular of cylindrical shape-preserving deformation exists for all angular spees and that, for problems (i) and (iii), there is no other solution. In connection with problems (ii) and (iii) values of the material constans are also given which correspond to the bifuraction or non-existence of soultions. Enegry consideration are used to determine the local stability of the various solutions obtained.

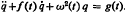An exact invariant is found for the one-dimensional oscillator with equation of motion . The method used is that of linear canonical transformations with time-dependent coeffcients. This is a new approach to the problem and has the advantage of simplicity. When f(t) and g(t) are zero, the invariant is related to the well-known Lewis invariant. The significance of extension to higher dimension of these results is indicated, in particular for the existence of non-invariance dynamical symmetry groups.

The point form of the conservation of energy equation is used to give simple and direct proof of results concerning the mean energy flux vector for systems of sinusoidal small amplitude waves in linear conservative systems. No constitutive equation is used explicitly.

A review of Heckmann and Schücking's formulation of Newtonian cosmology is presented, which permits the discussion of models more general than those possessing both homogeneity and isotropy. In particular it is shown that all homogeneous cosmologies may be uniquely specified by the rate of shear tensor as an arbitrary function of time and specifying arbitrary initial values for expansion, rotation and density. Perturbations of these models are now discussed, with a view to their possible implications for galaxy formation. The Jeans criterion is shown to hold in all these models, even in the presence of viscosity; this generalizes a result of Bonnor which only applied to the isotropic case. Furthermore, Bonnor's analysis is considerably simplified in the present paper. Finally, a WKB-type of approximation procedure is described which appears to be successful in estimating the growth rate of unstable fluctuations.