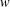 $w$-SHAPED STENOSED ARTERY USING THE GENERALIZED OLDROYD-B FLUID MODEL
$w$-SHAPED STENOSED ARTERY USING THE GENERALIZED OLDROYD-B FLUID MODELPublished online by Cambridge University Press: 21 July 2016
A theoretical study of an unsteady two-layered blood flow through a stenosed artery is presented in this article. The geometry of a rigid stenosed artery is assumed to be  $w$-shaped. The flow regime is assumed to be laminar, unsteady and uni-directional. The characteristics of blood are modelled by the generalized Oldroyd-B non-Newtonian fluid model in the core region and a Newtonian fluid model in the periphery region. The governing partial differential equations are derived for each region by using mass and momentum conservation equations. In order to facilitate numerical solutions, the derived differential equations are nondimensionalized. A well-tested explicit finite-difference method (FDM) which is forward in time and central in space is employed for the solution of a nonlinear initial boundary value problem corresponding to each region. Validation of the FDM computations is achieved with a variational finite element method algorithm. The influences of the emerging geometric and rheological parameters on axial velocity, resistance impedance and wall shear stress are displayed graphically. The instantaneous patterns of streamlines are also presented to illustrate the global behaviour of the blood flow. The simulations are relevant to haemodynamics of small blood vessels and capillary transport, wherein rheological effects are dominant.
$w$-shaped. The flow regime is assumed to be laminar, unsteady and uni-directional. The characteristics of blood are modelled by the generalized Oldroyd-B non-Newtonian fluid model in the core region and a Newtonian fluid model in the periphery region. The governing partial differential equations are derived for each region by using mass and momentum conservation equations. In order to facilitate numerical solutions, the derived differential equations are nondimensionalized. A well-tested explicit finite-difference method (FDM) which is forward in time and central in space is employed for the solution of a nonlinear initial boundary value problem corresponding to each region. Validation of the FDM computations is achieved with a variational finite element method algorithm. The influences of the emerging geometric and rheological parameters on axial velocity, resistance impedance and wall shear stress are displayed graphically. The instantaneous patterns of streamlines are also presented to illustrate the global behaviour of the blood flow. The simulations are relevant to haemodynamics of small blood vessels and capillary transport, wherein rheological effects are dominant.