Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-25T11:03:14.586Z Has data issue: false hasContentIssue false
  • English
  • Français

Stiff systems of ordinary differential equations. Part 1. Completely stiff, homogeneous systems

Published online by Cambridge University Press:  17 February 2009

J. J. Mahony  and
J. J. Shepherd
J. J. Mahony
Affiliation:
Department of Mathematics, University of Western Australia, Nedlands, Western Australia 6009
J. J. Shepherd
Affiliation:
Department of Mathematics, University of Western Australia, Nedlands, Western Australia 6009
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For the completely stiff real homogeneous system

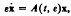
where e is a small positive parameter, a method is given for the construction of a basis for the solution space.

If A has n linearly independent eigenvector functions, then there exists a choice of these, {si}, with corresponding eigenvalue functions {λi}, such that there is a local basis for solution, that takes the form

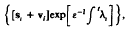
where vi is a vector that tends to zero with e. In general, a basis of this form exists only on an interval in which the distinct eigenvalues have their real parts ordered. A construction is provided for continuing any solution across the boundaries of any such interval. These results are proved for a finite or infinite interval for which there are only a finite number of points at which the ordering of the real parts of eigenvalues changes.

Type
Research Article
Information
The ANZIAM Journal , Volume 23 , Issue 1 , July 1981 , pp. 17 - 51
Copyright
Copyright © Australian Mathematical Society 1981

References

[1]Ackerberg, R. C. and O'malley, R. E., “Boundary layer problems exhibiting resonance”, Studies in Applied Math. 49 (1970), 277–295.CrossRefGoogle Scholar
[2]Chapman, P. and Mahony, J. J., “Reflection of waves in a slowly varying medium”, S.I.A.M. J. Appl. Math. 34 (1978), 303–319.Google Scholar
[3]Erdélyi, A. E., Asymptotic expansions (Dover, New York 1956).Google Scholar
[4]Liusternik, L. A. and Sobolev, V. J., Elements of functional analysis (Hindustan Publishing Corp., India, 1974).Google Scholar
[5]Nayfeh, A. H., Perturbation methods (John Wiley, New York, 1973).Google Scholar
[6]Shampine, L. F. and Gear, C. W., “A user's view of solving stiff ordinary differential equations”, S.I.A.M. Review 21 (1979), 1–17.Google Scholar
[7]Sibuya, Y., “Some global properties of matrices of functions of one variable”, Math. Annalen 161 (1965), 67–77.Google Scholar
[8]Smart, D. R., Fixed point theorems (Cambridge University Press, London, 1974).Google Scholar
[9]Vasil'eva, A. B., “The development of the theory of ordinary differential equations with a small parameter multiplying the highest derivative during the period 1966–1976”, Russian Math. Surveys 31 (1976), 109–131.Google Scholar
[10]Wasow, W., “Asymptotic expansion for ordinary differential equations: trends and problems” in Wilcox, Calvin H. (Ed.), Asymptotic solutions of differential equations and their applications, (John Wiley, New York, 1964).Google Scholar