Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-25T11:08:31.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Stiff systems of ordinary differential equations. III. Partially stiff systems

Published online by Cambridge University Press:  17 February 2009

J. J. Mahony  and
J. J. Shepherd
J. J. Mahony
Affiliation:
Department of Mathematics, University of Western Australia, Nedlands, Western Australia 6009
J. J. Shepherd
Affiliation:
Department of Mathematics, University of Western Australia, Nedlands, Western Australia 6009
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The partially stiff system of ordinary differential equations

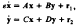
is studied by the methods developed in the earlier papers in this series. Here e is a small positive parameter, x and y are n- and m-vectors respectively, and A is nonsingular. A useful basis for the solution space of the homogeneous system is constructed and the method of variation of parameters is used to obtain useful representations of all solutions. Sufficient conditions are derived under which the formal approximation

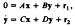
is close to the actual solution. it is found that purely imaginary eigenvalues for A require more stringent requirements for the formal technique to be valid. A brief discussion of the case when A is singular shows that there are a great number of possibilities requiring consideration for a general theory. it is suggested that local computation of such cases is likely to be the most effective weapon for any specific system.

Type
Research Article
Information
The ANZIAM Journal , Volume 23 , Issue 3 , January 1982 , pp. 310 - 331
Copyright
Copyright © Australian Mathematical Society 1982

References

[1]Erdélyi, A. E., Asymptotic expanions (Dover, New York, 1956).Google Scholar
[2]Mahony, J. J. and Shepherd, J. J., “Stiff systems of ordinaiy differential equations. I. Completely stiff homogeneous equations”, I. Austral. Math. Soc. B 23 (1981), 17–51.CrossRefGoogle Scholar
[3]Mahony, J. J. and Shepherd, J. J., “Stiff systems of ordinary differential equations. II. Boundary value problems for completely stiff systems”, J. Austral. Math. Soc. B 23 (1981), 136–172.CrossRefGoogle Scholar