Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T10:26:19.085Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability analysis of Runge–Kutta methods applied to a basic Volterra integral equation

Published online by Cambridge University Press:  17 February 2009

Christopher T. H. Baker  and
Joan C. Wilkinson
Christopher T. H. Baker
Affiliation:
Department of Mathematics, The University, Manchester, England
Joan C. Wilkinson
Affiliation:
Stanley Park Comprehensive School, Liverpool, England
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Our purpose in this paper is to display the stability analysis of Runge–Kutta methods applied to a Volterra integral equation of a simple form. As prerequisite we define, and then develop the structure of, the class of Runge–Kutta methods considered. The test equation is taken as the “;basic” equation 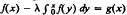; the simple form of this equation permits ready insight into features which are more obscure when considering (as elsewhere [1], [2], [6]) equations of a more complicated form. Due to the structure of the methods and the nature of the test equation, the stability analysis reduces to the study of recurrence relations of the form Фk + 1 = MФ k + γk (k = 0, 1, 2, …) which are common in stability discussions in numerical analysis.

Type
Research Article
Information
The ANZIAM Journal , Volume 22 , Issue 4 , April 1981 , pp. 515 - 538
Copyright
Copyright © Australian Mathematical Society 1981

References

[1]Amini, S. and Baker, C. T. H., “Further stability analysis of numerical methods for volterra integral equations of the second kind” University of Manchester, Numer. Anal. Tech. Rep. 47 (1980).Google Scholar
[2]Amini, S. and Baker, C. T. H., and Wilkinson, J. C., “Basic stability analysis of Runge—Kutta methods for Volterra integral equations of the second kind” University of Manchester, Numer. Anal. Tech. Rep. 46 (1980).Google Scholar
[3]Alexander, R., “Diagonally implicit Runge–Kutta methods for stiff o.d.e.'s” SIAM J. Numerical Analysis 14 (1977), 1006–1021.CrossRefGoogle Scholar
[4]Baker, C. T. H., The numerical treatment of integral equations (Clarendon Press, Oxford 1977; second printing 1978).Google Scholar
[5]Baker, C. T. H., Runge–Kutta methods for Volterra integral equations of the second kind (Lecture Notes in Mathematics No. 630 Springer-Verlag, 1978), 1–13.Google Scholar
[6]Baker, C. T. H., “Structure of recurrence relations in the study of stability in the numerical treatment of Volterra integral and integro-differential equations” J. of Integral Equations 2 (1980), 11–39.Google Scholar
[7]Baker, C. T. H. and Keech, M. S., “Stability regions in the numerical treatment of Volterra integral equations” SIAM J. Numerical Analysis 15 (1978), 394–417.CrossRefGoogle Scholar
[8]Baker, C. T. H., Makroglou, A., and Short, E., “Regions of stability in the numerical treatment of Volterra integro-differential equations” SIAM J. Numerical Analysis 16 (1979), 890–910.CrossRefGoogle Scholar
[9]Baker, C. T. H., Riddell, I. J., Keech, M. S., and Amini, S., Runge–Kulta methods with error estimates for Volterra integral equations of the second kind (ISNM Series No. 53 BirkÄuser-Verlag, Basel, 1980), 24–42.Google Scholar
[10]Baker, C. T. H. and Wilkinson, J. C., “Basic stability analysis of Runge—Kutta methods for Volterra integro-differential equations” University of Manchester, Numer. Anal. Tech. Rep.50 (1980).Google Scholar
[11]Bel'tyukov, B. A., “An analogue of the Runge—Kutta methods for this solution of a nonlinear integral equations of the Volterra type” Differential equations 1 (15), 417–433 (translation).Google Scholar
[12]Cash, J. R., “Diagonally implicit Runge—Kutta formulae with error estimates” J. Institute of Mathematics and its Applications 24 (1979), 293–301.CrossRefGoogle Scholar
[13]Donelson, J. III and Hansen, E., “Cyclic composite methods” SIAM J. Numerical Analysis 8 (1971), 137–157.CrossRefGoogle Scholar
[14]Hahn, W., Theory and application of Liapunov's direct method (Prentice-Hall, Englewood Cliffs, 1963).Google Scholar
[15]van der Houwen, P. J., Construction of integration formulas for initial value problems (North-Holland, Amsterdam 1977).Google Scholar
[16]van des Houwen, P. J., “On the numerical solution of Volterra integral equations of the second kind —I Stability; –II Runge—Kutta methods (with J. G. Blom)” Math. Centrum, Amsterdam. Reports NW 42/77 & 61/78.Google Scholar
[17]van der Houwen, P. J., “Convergence and stability results in Runge–Kutta type methods for Volterra integral equations of the second kind” BIT 20 (1980), 375–377.CrossRefGoogle Scholar
[18]Lambert, J. D., Computational methods in ordinary differential equations (Wiley, 1973).Google Scholar
[19]Lapidus, L. and Seinfeld, J. H., Numerical solution of ordinary differential equations (Academic, 1971).Google Scholar
[20]Miller, K. S., Linear difference equations (Benjamin, New York, 1968).CrossRefGoogle Scholar
[21]Pouzet, P., “Methode d'integration numerique des equations integrales et integro-differentielles du type de Volterra de seconde espece, Formules de Runge—Kutta” In Symposium on the numerical treatment of ordinary differential equations, integral equations and integro-differential equations (Birkhäuser, Basel, 1960), 362–368.Google Scholar
[22]Stetter, H. J., Analysis of discretization methods for ordinary differential equations (Springer-Verlag, Berlin, 1973).CrossRefGoogle Scholar
[23]Tsalyuk, Z. B., “Volterra integral equations” J. of Soviet Mathematics 12 (1979), 715–758 (in translation).CrossRefGoogle Scholar
[24]Varga, R. S., Matrix iterative analysis (Prentice-Hall, 1962).Google Scholar
[25]Wokenfelt, P. H. M., van der Houwen, P. J., and Baker, C. T. H., “Analysis of numerical methods for second kind Volterra equations by embedding techniques” Math. Centrum, Amsterdam, Report NW 71/79 (1979).Google Scholar