Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T10:38:06.859Z Has data issue: false hasContentIssue false
  • English
  • Français

Source solutions for the nonlinear diffusion-convection equation

Published online by Cambridge University Press:  17 February 2009

G. C. Sander ,
R. D. Braddock ,
I. F. Cunning ,
J. Norbury  and
S.W. Weeks
G. C. Sander
Affiliation:
Faculty of Science and Technology Griffith University, Nathan 4111, Australia
R. D. Braddock
Affiliation:
Faculty of Environmental Sciences Griffith University, Nathan 4111, Australia
I. F. Cunning
Affiliation:
Faculty of Environmental Sciences Griffith University, Nathan 4111, Australia
J. Norbury
Affiliation:
Mathematical Institute, Oxford University24–29 St Giles, Oxford, OX1 3LB
S.W. Weeks
Affiliation:
Faculty of Science and Technology Griffith University, Nathan 4111, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the paper King [8], a new class of source solutions was derived for the nonlinear diffusion equation for diffusivities of the form D(c) = D0cm/(l - vc)m+2. Here we extend this method for the nonlinear diffusion and convection equation

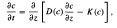
to obtain mass-conserving source solutions for a nonlinear conductivity function K(c) = K0cm+2/(l - vc)m+1. In particular we consider the cases m = -1,0, and 1, where fully analytical solutions are available. Furthermore we provide source solutions for the exponential forms of the diffusivity and conductivity as given by D(c) = D0c−2e−n/c and K(c) = K0ce−n/c.

Type
Research Article
Information
The ANZIAM Journal , Volume 39 , Issue 1 , July 1997 , pp. 28 - 45
Copyright
Copyright © Australian Mathematical Society 1997

References

[1] Broadbridge, P. and Rogers, C., “Exact solutions for vertical drainage and redistribution in soils”, J. Eng. Math. 24 (1990) 25–43.CrossRefGoogle Scholar
[2] Edwards, M. P., “Classical symmetry reductions of nonlinear diffusion – convection equations”, Phys. Lett. 190 (1994) 149–154.Google Scholar
[3] Fayer, M. J. and Simmons, C. S., “Modified soil water retention functions for all matric suctions”, Water Resour. Res. 31 (1995) 1233–1238.Google Scholar
[4] Fujita, H., “The exact pattern of a concentration - dependent diffusion in a semi - infinite medium, II”, Textile Res. J. 22 (1952) 823–827.Google Scholar
[5] Grundy, R. E., “The Cauchy problem for a nonlinear diffusion equation with absorption and convection”, IMA J. Appl. Math. 40 (1988) 183–204.Google Scholar
[6] Hill, J. M., “Similarity solutions for nonlinear diffusion in a new integration procedure”, J. Eng. Math. 23 (1989) 141–155.CrossRefGoogle Scholar
[7] L, W. Hogarth, Parlange, J.-Y. and Braddock, R. D., “First integrals of the infiltration equation. 2. Nonlinear conductivity”, Soil Sci. 148 (1989) 165–171.Google Scholar
[8] King, J. R., “Exact solutions to some nonlinear diffusion equations”, Q. J. Mech. Appl. Math. 42 (1989) 537–552.Google Scholar
[9] Kingston, J. G. and Rogers, C., “Reciprocal Backlund transformations of conservation laws”, Phys. Lett. 92 (1982) 261–264.Google Scholar
[10] Lisle, I. G. and Parlange, J.-Y., “Analytical reduction for a concentration dependent diffusion problem”, ZAMP 44 (1993) 85–102.Google Scholar
[11] Peletier, L. A., “A necessary and sufficient condition for the existence of an interface in flows through porous media”, Arch. Rat. Mech. Anal. 56 (1974) 183–190.Google Scholar
[12] Philip, J. R., “Theory of infiltration”, Adv. Hydro 5 (1969) 215–296.Google Scholar
[13] Philip, J. R., “Exact solutions for redistribution by nonlinear convection–diffusion”, J. Aust. Math. Soc. Ser. B 33 (1992) 363–383.Google Scholar
[14] Rogers, C., “Application of reciprocal Backlund transformations to a class of nonlinear boundary value problems”, J. Phys. A: Math. Gen. 16 (1983) L493–L495.Google Scholar
[15] Sander, G. C., “Exact solutions to nonlinear diffusion-convection problems on finite domains”, J. Aust. Math. Soc. Ser. B 33 (1991) 384–401.Google Scholar
[16] Sander, G. C., Cunning, I. F., Hogarth, W. L. and Parlange, J.-Y., “Exact solution for nonlinear, nonhysteretic redistribution in vertical soil of finite depth”, Water Resour. Res. 27 (1991) 1529–1536.Google Scholar
[17] Genuchten, R. van, “Predicting the hydraulic conductivity of unsaturated soils”, Soil Sci. Soc. Am. J. 44 (1980) 892–898.Google Scholar
[18] Warrick, A. W., Lomen, D. O. and Islas, A., “An anlytical solution to Richards' equation for a draining soil profile”, Water Resour. Res. 26 (1990) 253–258.Google Scholar
[19] Watson, K. K., Reginato, R. J. and Jackson, R. D., “Soil water hysteresis in a field soil”, Soil Sci. Soc. Am. Proc. 39 (1975) 242–246.Google Scholar
[20] Watson, K. K. and Sardana, V., “Numerical study of the effect of hysteresis on post infiltration redistribution”, in Intern. Conf. on Infiltration Development and Application, Univ of Hawaii, Jan 6, 1987).Google Scholar
[21] Yung, C. M., Verburg, K. and Baveye, P., “Group classification and symmetry reductions of the nonlinear diffusion - convection equation u1 = (d(u)ux)x - K1(u)ux”, Int. J. Non-Linear Mech. 29 (1994) 273–278.Google Scholar