Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T11:03:32.969Z Has data issue: false hasContentIssue false
  • English
  • Français

solutions of period three for a non-linear difference equation

Published online by Cambridge University Press:  17 February 2009

A. Brown
A. Brown
Affiliation:
Department of Theoretical Physics, Research School of Physical Sciences, Australian National University, G.P.O. Box 4, Canberra, A.C.T. 2601.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The paper uses the factorisation method to discuss solutions of period three for the difference equation

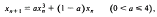
which has been proposed as a simple mathematical model for the effect of frequency dependent selection in genetics. Numerical values are obtained for the critical values of a at which solutions of period three first appear. In addition, the interval in which stable solutions are possible has been determined. Exact solutions are given for the case a = 4 and these have been used to check the results.

Type
Research Article
Information
The ANZIAM Journal , Volume 25 , Issue 4 , April 1984 , pp. 451 - 462
Copyright
Copyright © Australian Mathematical Society 1984

References

[1]Brown, A., “Equations for periodic solutions of a logistic difference equation”, J. Austral. Math. Soc. Ser. B 23 (1981), 78–94.CrossRefGoogle Scholar
[2]Brown, A., “Solutions of period seven for a logistic difference equation”, Bull. Austral. Math. Soc. 26 (1982), 263–284.Google Scholar
[3]Clarke, B. C., “Frequency-dependent and density-dependent natural selection”, in The role of natural selection in human evolution (ed. Salzano, F. M.), (North-Holland, Amsterdam, 1975), 187–200.Google Scholar
[4]Clarke, B. C., “The evolution of genetic diversity”, Proc. Roy. Soc. London Ser. B 205 (1979), 453–474.Google Scholar
[5]Falconer, D. S., Introduction to quantitative genetics (Longman, London, 2nd edition, 1981), 43.Google Scholar
[6]Frauenthal, J. C., Introduction to population modeling (Birkhäuser, Basel, 1980), 71–73.Google Scholar
[7]Lewontin, R. C., The genetic basis of evolutionary change (Columbia Univ. Press, New York, 1974), 256–260.Google Scholar
[8]May, R. M., “Bifurcations and dynamic complexity in ecological systems”, Ann. N. Y. Acad. Sci. 316 (1979), 517–529.Google Scholar
[9]May, R. M., “Non-linear problems in ecology and resource management”, Lecture notes for Les Houches Summer School on “Chaotic Behaviour of Deterministic Systems”, July 1981.Google Scholar
[10]Parkin, D. T., An introduction to evolutionary genetics (Arnold, London, 1979), 81, 99–110.Google Scholar