No CrossRef data available.
Published online by Cambridge University Press: 17 February 2009
The general solution of the rth inhomogeneous linear difference equation is given in the form
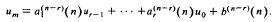
The coefficients 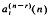 , i = 2, …, r, and b(n−r)(n) can be evaluated from n values
, i = 2, …, r, and b(n−r)(n) can be evaluated from n values 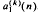 , k = 0, …, n − 1, which santisfy an rth order homogenous linear difference equation. In the rth order homogeneous case and if n ≥ 2r, the method requires the evaluation of r determinants of successive orders n − 2r + 1, n − 2r + 2, …, n − r. If r ≤ n ≤ 2r − 1, only n − r determinants are required, with orders varying from 1 to n − r. In the second order ihnomogenous case,
, k = 0, …, n − 1, which santisfy an rth order homogenous linear difference equation. In the rth order homogeneous case and if n ≥ 2r, the method requires the evaluation of r determinants of successive orders n − 2r + 1, n − 2r + 2, …, n − r. If r ≤ n ≤ 2r − 1, only n − r determinants are required, with orders varying from 1 to n − r. In the second order ihnomogenous case, 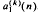 can be evaluated from a continued fraction amd a simple product.
can be evaluated from a continued fraction amd a simple product.