Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-17T08:19:55.941Z Has data issue: false hasContentIssue false
  • English
  • Français

SCHEDULING ON TWO PARALLEL MACHINES WITH TWO DEDICATED SERVERS

Part of: Operations research and management science

Published online by Cambridge University Press:  25 May 2017

YIWEI JIANG Open the ORCID record for YIWEI JIANG [Opens in a new window] ,
PING ZHOU ,
HUIJUAN WANG  and
JUELIANG HU Open the ORCID record for JUELIANG HU [Opens in a new window]
YIWEI JIANG
Affiliation:
College of Finance and Trade, Ningbo Dahongying University, Ningbo 315175, China email [email protected] School of Sciences, Zhejiang Sci-Tech University, Hangzhou 310018, China email [email protected]
PING ZHOU
Affiliation:
College of Humanities, Zhejiang Business College, Hangzhou 310053, China
HUIJUAN WANG
Affiliation:
School of Sciences, Zhejiang Sci-Tech University, Hangzhou 310018, China email [email protected]
JUELIANG HU*
Affiliation:
School of Sciences, Zhejiang Sci-Tech University, Hangzhou 310018, China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study a nonpreemptive scheduling on two parallel identical machines with a dedicated loading server and a dedicated unloading server. Each job has to be loaded by the loading server before being processed on one of the machines and unloaded immediately by the unloading server after its processing. The loading and unloading times are both equal to one unit of time. The goal is to minimize the makespan. Since the problem is NP-hard, we apply the classical list scheduling and largest processing time heuristics, and show that they have worst-case ratios, 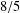$8/5$ and 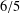$6/5$, respectively.

Keywords

schedulingserveralgorithmworst-case ratiomakespan

MSC classification

Primary: 90B35: Scheduling theory, deterministic
Secondary: 90C27: Combinatorial optimization
Type
Research Article
Information
The ANZIAM Journal , Volume 58 , Issue 3-4 , April 2017 , pp. 314 - 323
Copyright
© 2017 Australian Mathematical Society 

References

Batur, G., Karasan, O. and Akturk, M., “Multiple part-type scheduling in flexible robotic cells”, Int. J. Product. Econ. 135 (2012) 726–740; doi:10.1016/j.ijpe.2011.10.006.Google Scholar
Brucker, P., Dhaenens-Flipo, C., Knust, S., Kravchenko, S. A. and Werner, F., “Complexity results for parallel machine problems with a single server”, J. Sched. 5 (2002) 429–457; doi:10.1002/jos.120.CrossRefGoogle Scholar
Hall, N., Potts, C. and Sriskandarajah, C., “Parallel machine scheduling with a common server”, Discrete Appl. Math. 102 (2000) 223–243; doi:10.1016/S0166-218X(99)00206-1.CrossRefGoogle Scholar
Jiang, Y., Dong, J. and Ji, M., “Preemptive scheduling on two parallel machines with a single server”, Comput. Ind. Eng. 66 (2013) 514–518; doi:10.1016/j.cie.2013.07.020.Google Scholar
Jiang, Y., Wang, H. and Zhou, P., “An optimal preemptive algorithm for the single-server parallel-machine scheduling with loading and unloading times”, Asia-Pac. J. Oper. Res. 32 (2014) 11 pages; doi:10.1142/S0217595914500390.Google Scholar
Jiang, Y., Yu, F., Zhou, P. and Hu, J., “Online algorithms for scheduling on two parallel machines with a single server”, Int. Trans. Oper. Res. 22 (2015) 913–927; doi:10.1111/itor.12136.Google Scholar
Jiang, Y., Zhang, Q., Hu, J., Dong, J. and Ji, M., “Single-server parallel-machine schduling with loading and unloading times”, J. Comb. Optim. 30 (2015) 201–213; doi:10.1007/s10878-014-9727-z.Google Scholar
Kim, M. Y. and Lee, Y. H., “MIP models and hybrid algorithm for minimizing the makespan of parallel machines scheduling problem with a single server”, Comput. Oper. Res. 39 (2012) 2457–2468; doi:10.1016/j.cor.2011.12.011.Google Scholar
Koulamas, C., “Scheduling two parallel semiautomatic machines to minimize machine interference”, Comput. Oper. Res. 23 (1996) 945–956; doi:10.1016/0305-0548(96)00011-1.Google Scholar
Kravchenko, S. and Werner, F., “Parallel machine scheduling problems with a single server”, Math. Comput. Modelling 26 (1997) 1–11; doi:10.1016/S0895-7177(97)00236-7.Google Scholar
Ou, J., Qi, X. and Lee, C., “Parallel machine scheduling with multiple unloading servers”, J. Sched. 13 (2010) 213–226; doi:10.1007/s10951-009-0104-1.CrossRefGoogle Scholar
Su, C., “Online LPT algorithms for parallel machines scheduling with a single server”, J. Comb. Optim. 26 (2013) 480–488; doi:10.1007/s10878-011-9441-z.CrossRefGoogle Scholar
Wang, G. and Cheng, T. C. E., “An approximation algorithm for parallel machine scheduling with a common server”, J. Oper. Res. Soc. 52 (2001) 234–237; doi:10.1057/palgrave.jors.2601074.Google Scholar
Werner, F. and Kravchenko, S., “Scheduling with multiple servers”, Autom. Remote Control 71 (2010) 2109–2121; doi:10.1134/S0005117910100103.Google Scholar
Xie, X., Li, Y., Zhou, H. and Zheng, Y., “Scheduling parallel machines with a single server”, in: Measurement, information and control (MIC) (IEEE, Harbin, China, 2012) 453–456; doi:10.1109/MIC.2012.6273340.Google Scholar
Zhang, L. and Wirth, A., “On-line scheduling of two parallel machines with a single server”, Comput. Oper. Res. 36 (2009) 1529–1553; doi:10.1016/j.cor.2008.02.015.CrossRefGoogle Scholar