Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chou, J. H.
Hsia, Wei-Shen
and
Lee, Tan-Yu
1985.
Second order optimality conditions for mathematical prograramming with set functions.
The Journal of the Australian Mathematical Society. Series B. Applied Mathematics,
Vol. 26,
Issue. 3,
p.
284.
Chou, J.H
Hsia, Wei-Shen
and
Lee, Tan-Yu
1985.
On multiple objective programming problems with set functions.
Journal of Mathematical Analysis and Applications,
Vol. 105,
Issue. 2,
p.
383.
Corley, H.W
1987.
Optimization theory for n-set functions.
Journal of Mathematical Analysis and Applications,
Vol. 127,
Issue. 1,
p.
193.
Hsia, W. S.
and
Lee, T. Y.
1987.
ProperD-solutions of multiobjective programming problems with set functions.
Journal of Optimization Theory and Applications,
Vol. 53,
Issue. 2,
p.
247.
Lai, Hang-Chin
and
Lin, Lai-Jui
1988.
The Fenchel-Moreau theorem for set functions.
Proceedings of the American Mathematical Society,
Vol. 103,
Issue. 1,
p.
85.
Lai, Hang-Chin
and
Lin, Lai-Jiu
1988.
Moreau-Rockafellar type theorem for convex set functions.
Journal of Mathematical Analysis and Applications,
Vol. 132,
Issue. 2,
p.
558.
Zaimai, G.J.
1989.
Optimality conditions and duality for constrained measurable subset selection problems with minmax objective functions.
Optimization,
Vol. 20,
Issue. 4,
p.
377.
Lee, Tan-Yu
1989.
Generalized convex set functions.
Journal of Mathematical Analysis and Applications,
Vol. 141,
Issue. 1,
p.
278.
Lai, H. C.
and
Lin, L. J.
1989.
Optimality for set functions with values in ordered vector spaces.
Journal of Optimization Theory and Applications,
Vol. 63,
Issue. 3,
p.
371.
Lin, Lai-Jiu
1990.
Optimality of differentiable, vector-valued n-set functions.
Journal of Mathematical Analysis and Applications,
Vol. 149,
Issue. 1,
p.
255.
Zalmai, G.J
1990.
Sufficiency criteria and duality for nonlinear programs involving n-set functions.
Journal of Mathematical Analysis and Applications,
Vol. 149,
Issue. 2,
p.
322.
Zalmai, G.J
1990.
Duality for generalized fractional programs involving n-set functions.
Journal of Mathematical Analysis and Applications,
Vol. 149,
Issue. 2,
p.
339.
Lin, Lai-Jiu
1991.
Duality theorems of vector-valued n-set functions.
Computers & Mathematics with Applications,
Vol. 21,
Issue. 11-12,
p.
165.
Hsia, Wei-Shen
Lee, Jae Hai
and
Lee, Tan-Yu
1991.
Convolution of Set Functions.
Rocky Mountain Journal of Mathematics,
Vol. 21,
Issue. 4,
Preda, V.
1991.
Oil minmax programming problems containing n-set functions.
Optimization,
Vol. 22,
Issue. 4,
p.
527.
Zalmai, G.J.
1991.
Optimality conditions and duality for multiobjective measurable subset selection problems.
Optimization,
Vol. 22,
Issue. 2,
p.
221.
Lin, Lai-Jiu
1991.
On the optimality conditions of vector-valued n-set functions.
Journal of Mathematical Analysis and Applications,
Vol. 161,
Issue. 2,
p.
367.
Lin, Lai-Jiu
1992.
On the optimality of differentiable nonconvex n-set functions.
Journal of Mathematical Analysis and Applications,
Vol. 168,
Issue. 2,
p.
351.
Bhatia, D.
and
Tewari, S.
1993.
Multiobjective Fractional Duality Forn-Set Functions.
Journal of Information and Optimization Sciences,
Vol. 14,
Issue. 3,
p.
321.
Lai, H. C.
and
Szilágyi, P.
1994.
Alternative theorems and saddlepoint results for convex programming problems of set functions with values in ordered vector spaces.
Acta Mathematica Hungarica,
Vol. 63,
Issue. 3,
p.
231.


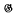 ,
, 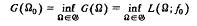
 (for the definition, see the later context).
(for the definition, see the later context).