Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-25T02:49:21.455Z Has data issue: false hasContentIssue false
  • English
  • Français

Reduction of second order linear dynamical systems, with large dissipation, by state variable transformations

Published online by Cambridge University Press:  17 February 2009

R. B. Leipnik
R. B. Leipnik
Affiliation:
Department of Mathematics, University of California, Santa Barbara, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Linear dynamical systems of the Rayleigh form 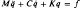are transformed by linear state variable transformations 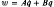, where A and B are chosen to simplify analysis and reduce computing time. In particular, A is essentially a square root of M, and B is a Lyapunov quotient of C by A. Neither K nor C is required to be symmetric, nor is C small. The resulting state-space systems are analysed by factorisation of the evolution matrices into reducible factors. Eigenvectors and eigenvalues are determined by these factors. Conditions for further simplification are derived in terms of Kronecker determinants. These results are compared with classical reductions of Rayleigh, Duncan, and Caughey, which are reviewed at the outset.

Type
Research Article
Information
The ANZIAM Journal , Volume 32 , Issue 2 , October 1990 , pp. 207 - 222
Copyright
Copyright © Australian Mathematical Society 1990

References

[1]Bartels, R. H. and Stewart, G. W., “Solution of the matrix equation AX + XB = C (Algorithm 826)”, Commun. of Assoc, of Comp. Mach. 15 (1972) 820–826.Google Scholar
[2]Bellman, R., Introduction to Matrix Analysis (McGraw Hill, New York, 1960).Google Scholar
[3]Brandon, J. A., “Discussion of alternative Duncan formulations of the eigenproblem for the solution of non-classically, viscously damped linear systems”, Trans ASME, Ser. E, J. of Applied Mechanics 51,4 (1985) 605–609.Google Scholar
[4]Caughey, T. K. and O'Kelly, M. E. J., “Classical normal modes in damped linear systems”, Trans ASME, Ser. E, J. of Applied Mechanics 32,3 (1965) 583–588.CrossRefGoogle Scholar
[5]Duncan, W. J. et al. , Elementary matrices and some applications to dynamics and differential equations (Macmillian, New York, 1946, reprint).Google Scholar
[6]Frank, P. and von Mises, R., Partial differential equations of physics (Dover, New York, 1961, reprint).Google Scholar
[7]Gantmacher, F. R., Theory of matrices Vol. I and II (Chelsea, New York, 1959, reprint).Google Scholar
[8]Hamel, G., Theoretische Mechanik (Springer, Berlin, 1949).CrossRefGoogle Scholar
[9]Landau, L. D., Course of theoretical physics - quantum mechanics (Pergamon Press, London, 1982).Google Scholar
[10]Lax, P. D., Non-linear differential equations in applied science (Elsevier, New York, 1983).Google Scholar
[11]Leipnik, R. B., “Extension of Newman's formula for the Sylvester equation to the generic case”, Linear and Multilinear Algebra 12,4 (1982/1983) 305–309.CrossRefGoogle Scholar
[12]Piccinini, L. C. et al. , Ordinary differential equations in Rn (Springer, Berlin, 1984).CrossRefGoogle Scholar
[13]Rayleigh, J. W. S., Theory of sound (Dover, New York, 1945, reprint).Google Scholar
[14]Stewart, G. W. and Duff, I. S., “Practical comparisons of codes for the solution of sparse linear systems”, in Sparse matrix computation symposium (eds. Stewart, G.W. and Duff, I.S.) (SIAM Press, Philadelphia, 1976).Google Scholar
[15]Toda, N., Theory of non-linear lattices (Springer, Berlin, 1, 1981).CrossRefGoogle Scholar
[16]Vance, J. M. and Sitchin, A., “Derivation of first order difference equations for dynamical systems by direct applications of Hamilton's principle”, Trans ASME, Ser. E, J. of Applied Mechanics 37, 2 (1970) 276–278.CrossRefGoogle Scholar
[17]van Loan, C. F. and Golub, G. H. et al. , “A Hessenberg-Schur method for the solution of AX + XB = C”, SIAM J. on Num. Anal. 17 (1980) 883–893.Google Scholar