Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bai, Yanqin
Xie, Wei
and
Zhang, Jing
2012.
New parameterized kernel functions for linear optimization.
Journal of Global Optimization,
Vol. 54,
Issue. 2,
p.
353.
Lee, Yong-Hoon
Cho, You-Young
and
Cho, Gyeong-Mi
2013.
Kernel function based interior-point methods for horizontal linear complementarity problems.
Journal of Inequalities and Applications,
Vol. 2013,
Issue. 1,
Kheirfam, Behrouz
2014.
A Generic Interior-point Algorithm for Monotone Symmetric Cone Linear Complementarity Problems Based on a New Kernel Function.
Journal of Mathematical Modelling and Algorithms in Operations Research,
Vol. 13,
Issue. 4,
p.
471.


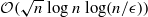 and
and 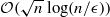 iteration bounds for large-update and small-update methods, respectively, which are currently the best known bounds for such methods.
iteration bounds for large-update and small-update methods, respectively, which are currently the best known bounds for such methods.