Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-25T10:08:08.586Z Has data issue: false hasContentIssue false
  • English
  • Français

Partial differential equations for Eigenvalues: sensitivity and perturbation analysis

Published online by Cambridge University Press:  17 February 2009

Roy B. Leipnik
Roy B. Leipnik
Affiliation:
University of California at Santa Barbara.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The well-known Wilkinson expressions for the first derivatives of (ordinary) eigen-values and eigenvectors of simple matrices, in terms of the set of eigenvalues and eigenvectors, are redifferentiated and combined to obtain partial differential equations for the eigenvalues. Analogous expressions are obtained for the first derivatives of generalised eigenvalues and eigenvectors of simple pairs of matrices (A, B), defined by 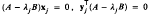. Again, redifferentiation and combination yields slightly more complicated partial differential equations for the generalised eigenvalues. When the matrices depend on a few parameters θ1, θ2, …, the resulting differential equations for the eigenvalues, with those parameters as independent variables, can easily be derived. These parametric equations are explicit representations of analytic perturbation results of Kato, expressed by him as rather abstract complex matrix integrals. Connections with bounds for eigenvalues derived by Stewart and Sun can also be made. Two applications are exhibited, the first being to a broken symmetry problem, the second being to working out the second-order perturbations for a classical problem in the theory of waves in cold plasmas.

Type
Research Article
Information
The ANZIAM Journal , Volume 34 , Issue 4 , April 1993 , pp. 439 - 470
Copyright
Copyright © Australian Mathematical Society 1993

References

[1] Bargman, R. E. and Nel, D. G., “On the matrix differentiation of the characteristic roots of matrices”, S. Afr. Statistic J. 13 (1974) 135–144.Google Scholar
[2] Bauer, F. L. and Fike, C. T., “Norms and exclusion theorems”, Numerische Mathematik 2 (1960) 42–43.CrossRefGoogle Scholar
[3] Baumgärtel, H., Endlichdimensionale analytische Störungstheorie (Akademie-Verlag, Berlin, 1972).Google Scholar
[4] Bhatia, R., Perturbation Bounds Research for Matrix Eigenvalues (Pitman Publishing, Harlow, Essex, U.K., 1987).Google Scholar
[5] Crawford, C. R., “A stable generalized eigenvalue problem”, SIAM J. Numer. Anal. 13 (1976) 854–860.CrossRefGoogle Scholar
[6] Elsner, L., “On the variation of the spectra of matrices”, Linear Algebra and its Applications 47 (1982) 128–138.CrossRefGoogle Scholar
[7] Gantmacher, F. R., The Theory of Matrices, (vol. 1 (transl. 1959), vol. II (transl. 1960), Chelsea Publishing, New York).Google Scholar
[8] Henrici, P., “Bounds for iterates, inverses, and fields of values of non-normal matrices,” Numerische Mathematik 4 (1962) 24–39.CrossRefGoogle Scholar
[9] Householder, W. T., Theory of Matrices in Numerical Analysis (Ginn-Blaisdell, Boston, 1964); reprinted Dover Publishing, New York, 1975).Google Scholar
[10] Kato, T., A Short Introduction to Perturbation Theory for Linear Operators (Springer-Verlag, New York, 1982).CrossRefGoogle Scholar
[11] Ostrowski, A., “Über die Stetigkeit von charakteristischen Wurzeln in Abhandigkeit von den Matrizenelementon”, Jahresbericht der Deutsch Math. Verein 60 (1957), 40–42.Google Scholar
[12] Rogers, G. S., Matrix Derivatives (M. Dekker, New York, 1980).Google Scholar
[13] Stewart, G. W., “On the sensitivity of the eigenproblem Ax = λBx”, SIAM J. Numer. Anal. 4 (1972), 669–686.CrossRefGoogle Scholar
[14] Stewart, G. W., “Gerschgorin theory in the generalised eigenvalue problem Ax = λBx”, Math. of Comp. 29 (1975) 600–606.Google Scholar
[15] Stewart, W. G., “A second-order perturbation expansion for small singular values”, Linear Algebra and its Applications 56 (1984) 23–35.CrossRefGoogle Scholar
[16] Stewart, G. W. and Sun, J. G., Matrix Perturbation Theory (Academic Press, New York, 1990).Google Scholar
[17] Stix, T. H., The Theory of Plasma Waves (McGraw-Hill, New York, 1962).Google Scholar
[18] Sun, J. G., Perturbation Analysis for Generalized Eigenproblems and Generalized Singular Value Problems, Matrix Pencils (Kagstron, and Ruhe, , eds.), (Springer-Verlag, Berlin, 1983).Google Scholar
[19] Sun, J. G., “Perturbation bounds for eigenspaces of a definite matrix pair”, Numerische Mathematik 41 (1983) 321–343.CrossRefGoogle Scholar
[20] Wilkinson, J. H., The Algebraic Eigenvalue Problem (Clarendon Press, Oxford, 1965).Google Scholar