Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T11:29:17.671Z Has data issue: false hasContentIssue false
  • English
  • Français

Parseval's integral and the Jacobi expansions in series of Bessel fuinctions

Published online by Cambridge University Press:  17 February 2009

John Lekner
John Lekner
Affiliation:
Physics Department, Victoria University of Wellington, Wellington, New Zealand.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The sums

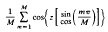
are shown to approximate J0 (z); the error terms are series in higher order Bessel functions, leading with J2M (z). Similar sums approximate J1(z). These sums may be looked on as extensions of the Jacobi expansions for cos z and sin z in series of Bessel functions. They become numerically useful for M > |z|.

Type
Research Article
Information
The ANZIAM Journal , Volume 27 , Issue 3 , January 1986 , pp. 370 - 375
Copyright
Copyright © Australian Mathematical Society 1986

References

[1]Born, M. and Wolf, E., Principles of optics (Pergamon Press, Oxford, 1965).Google Scholar
[2]Olver, F. W. J., Chapter 9 in Handbook of mathematical functions, edited by Abramowitz, M. and Stegun, I. A. (N.B.S. Applied Mathematics Series No. 55, 1964).Google Scholar
[3]Watson, G. N., Theory of Bessel functions (Cambridge University Press, 1966).Google Scholar