Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-22T07:41:04.324Z Has data issue: false hasContentIssue false
  • English
  • Français

On the topology of parametric optimal control

Published online by Cambridge University Press:  17 February 2009

Gerhard-W. Weber
Gerhard-W. Weber
Affiliation:
Department of Mathematics, Darmstadt University of Technology, Darmstadt, Germany.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We will study one-parameter families 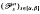of differentiable optimal control problems given by:

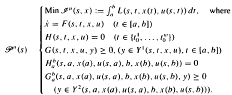
Here, at given times t the inequality constraint functions are of semi-infinite nature, the objective functional may also be of max-type. For each s ∈ ℝ the problem 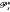is equivalent to a one-parameter family (Ps (t))t∈[a,b] of differentiable optimization problems. From these the consideration of generalized critical trajectories, such as a local minimum trajectory, comes into our investigation. According to a concept introduced by Hettich, Jongen and Stein in optimization, we distinguish eight types of generalized critical trajectories. Under suitable continuity, compactness and integrability assumptions, those problems, which exclusively have generalized critical points being of one of these eight types, are generic. We study normal forms and characteristic examples, locally around these trajectories.

Moreover, we indicate the related concept of structural stability of optimal control problems 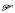due to the topological behaviour of the lower level sets under small data perturbations. Finally, we discuss the numerical consequences of our investigations for pathfollowing techniques with jumps.

Type
Research Article
Information
The ANZIAM Journal , Volume 39 , Issue 4 , April 1998 , pp. 463 - 497
Copyright
Copyright © Australian Mathematical Society 1998

References

[1]Allgower, E. and Georg, K., Introduction to Numerical Continuation Methods (Springer, 1990).Google Scholar
[2]Amann, H., Gewöhnliche Differentialgleichungen (Walter de Gruyter, 1979).Google Scholar
[3]Antipin, A. S., “Proximal differential systems with feedback control”, Russian Acad. Sci. Dokl. Math. 47 (1993) 183–186.Google Scholar
[4]Arutyunov, A. V. and Tynyanskil, N. T., “On necessary conditions for a local minimum in optimal control theory”, Soviet Math. Dokl. 29 (1984) 176–179.Google Scholar
[5]Arutyunov, A. V., Silin, D. B. and Zerkalov, L. G., “Maximum principle and second-order conditions for minimax problems of optimal control”, J. Optimization Theory and Applications 75 (1992). 521–533.CrossRefGoogle Scholar
[6]Avakov, E. R., Agrachev, A. A. and Arutyunov, A. V., “The level set of a smooth mapping in a neighbourhood of a singular point, and zeros of a quadratic mapping”, Math. USSR Sbornik 73 (1992) 455–466.CrossRefGoogle Scholar
[7]Bank, B., Guddat, J., Klatte, D., Kummer, B. and Tammer, K., Non-Linear Parametric Optimization (Akademie-Verlag, Berlin, 1982).Google Scholar
[8]Bröcker, Th. and Lander, L., Differentiable Germs and Catastrophes, London Math. Society Lecture Note Series 17 (Cambridge University Press, 1975).Google Scholar
[9]Chen, L.-Y., Goldenfeld, N., Oono, Y. and Paquette, G., “Selection, stability and renormalization”, Physica A204 (1994) 111–133.Google Scholar
[10]Chen, L.-Y., Goldenfeld, N. and Oono, Y., “Renormalization group theory for global asymptotic analysis”, preprint. University of Illinois at Urbana-Champaign (1994).Google Scholar
[11]Diener, I., “Trajectory nets connecting all critical points of a smooth function”, Mathematical Programming (1986) 340–352.Google Scholar
[12]Diener, I., Clobale Aspekte des kontinuierlichen Newton-Veifahrens (Habilitationsschrift, University of Gottingen, Germany, 1994).Google Scholar
[13]Dress, A. W. M., “Die Formensprache der Natur als Gegenstand der Mathematik”, Forschung ander Universität Bielefeld 5. University of Bielefeld (1992).Google Scholar
[14]Dress, A. W. M., Huson, D. and Müller, A., “Symmetric und Topologie von Riesenmolekülen, supramolekularen Clustern und Kristallen”, preprint. University of Bielefeld (1993).Google Scholar
[15]Evans, L. C. and Spruck, J., “Motion of level sets by mean curvature I.”, J. Differential Geometry 33 (1991) 635–681.Google Scholar
[16]Frauenfelder, H. and Wolynes, P. G., “Biomolecules: where the physics of complexity and simplicity meet”, Physics Today (1994) 58–64.Google Scholar
[17]Guddat, J., Jongen, H.Th. and Rückmann, J., “On stability and stationary points in nonlinear optimization”, J. Austral. Math. Soc. Ser. B 28 (1986) 36–56.Google Scholar
[18]Guddat, J. and Jongen, H.Th., “Structural stability in nonlinear optimization”, Optimization 18 (1987) 617–631.Google Scholar
[19]Vasquez, F. Guerre, Guddat, J. and Jongen, H.Th., Parametric Optimization: Singularities, Pathfol- lowing and Jumps (John Wiley, 1990).Google Scholar
[20]Hettich, R., Jongen, H.Th. and Stein, O., “On continuous deformations of semi-infinite optimization problems”, in Approximation and Optimization in the Caribbean II (eds. Florenzano, M., Guddat, J., Jimenez, M., Jongen, H.Th., Lagomasino, G. Lopez and Marcellan, F.), (Peter Lang Verlag, Frankfurt a.M., 1995), 406–424.Google Scholar
[21]Hettich, R. and Zencke, P., Numehsche Methoden der Approximation und semi-infmiten Optimierung (Teubner Studienbücher, Stuttgart, 1982).CrossRefGoogle Scholar
[22]Hirsch, M. W., Differential Topology (Springer Verlag, 1976).Google Scholar
[23]Hunt, B. R., Sauer, T. and Yorke, J. A., “Prevalence: a translation-invariant “almost every” on infinite dimensional spaces”. Bulletin of the American Mathematical Society 27 (1992) 217–238.Google Scholar
[24]Hurd, A. E. and Loeb, P. A., An Introduction to Nonstandard Real Analysis (Academic Press, Inc., 1985).Google Scholar
[25]Ibragimov, N. H., “Sophus Lie and harmony in mathematical physics, on the 150th anniversary of his birth”, The Mathematical Intelligencer 16 (1994) 20–28.Google Scholar
[26]Ilmanen, T., “The level-set flow on a manifold”, Proc. Symposia in Pure Mathematics 54, part I (1993) 193–203.CrossRefGoogle Scholar
[27]Jongen, H.Th., Jonker, P. and Twilt, F., Nonlinear Optimization in R″. I. Morse Theory, Chehychev Approximation (Peter Lang Verlag, Frankfurt a.M., Bern, New York, 1983).Google Scholar
[28]Jongen, H.Th., Jonker, P. and Twilt, F., Nonlinear Optimization in R″. II. Transversalily. Flows. Parametric Aspects (Peter Lang Verlag, Frankfurt a.M., Bern, New York, 1986).Google Scholar
[29]Jongen, H.Th., Jonker, P. and Twilt, F., “One-parameter families of optimization problems: equality constraints”, J. Optimization Theory and Applications 48 (1986) 141–161.CrossRefGoogle Scholar
[30]Jongen, H.Th., Jonker, P. and Twilt, F., “Critical sets in parametric optimization”, Mathematical Programming 34 (1986) 333–353.Google Scholar
[31]Jongen, H.Th., Jonker, P. and Twilt, F., “A note on Branin's method for finding the critical point of smooth function”, in Parametric Optimization and Related Topics (ed. Guddat, J. et al.), (Akademie- Verlag, Berlin, 1987) 209–228.Google Scholar
[32]Jongen, H.Th. and Pallaschke, D., “On linearization and continuous selections of functions”, Optimization 19 (1988) 343–353.Google Scholar
[33]Jongen, H.Th., Twilt, F. and Weber, G.-W., “Semi-infinite optimization: structure and stability of the feasible set”, J. Optimization Theory and Applications 72 (1992) 529–552.CrossRefGoogle Scholar
[34]Jongen, H.Th., Rückmann, J.-J. and Weber, G.-W., “One-parametric nonlinear optimization: on the stability of the feasible set”, SI AM J. Optimization 4 (1994) 637–648.Google Scholar
[35]Jongen, H.Th. and Stein, O., “On generic one-parametric semi-infinite optimization”, preprint. University of Trier, Trier, Germany (1995).Google Scholar
[36]Jongen, H.Th. and Weber, G.-W., “On parametric nonlinear programming”, Annals of Operations Research 27 (1990) 253–284.Google Scholar
[37]Jongen, H.Th. and Weber, G.-W., “Nonlinear optimization: characterization of structural stability”, J. Global Optimization 1 (1991) 47–64.Google Scholar
[38]Jongen, H.Th. and Weber, G.-W., “Nonconvex optimization and its structural frontiers”, in Modern Methods of Optimization (eds. Krabs, W. and Zowe, J.), Lecture Notes in Econom. and Math. Systems 378 (1992) 151–203.CrossRefGoogle Scholar
[39]Jongen, H.Th. and Weber, G.-W., personal communication, 1994.Google Scholar
[40]Jongen, H.Th. and Zwier, G., “On the local structure of the feasible set in semi-infinite optimization”, in Parametric Optimization and Approximation (eds. Brosowski, B. and Deutsch, F.), ISNM 72, (Birkhäuser Verlag, Basel-Boston-Stuttgart, 1985) 185–202.CrossRefGoogle Scholar
[41]Jongen, H.Th. and Zwier, G., “On regular semi-infinite optimization”, in Infinite Programming (eds. Anderson, E. J. and Philpott, A. B.), Lecture Notes in Econom. and Math. Systems 259, (Springer Verlag, 1985) 53–64.CrossRefGoogle Scholar
[42]Klötzler, R., “TransportfluB-Optimierung”, GMÖOR Newsletter 2 (1994) 3–10.Google Scholar
[43]Kojima, M., “Strongly stable stationary solutions in nonlinear programs”, in Analysis and Compulation of Fixed Points (ed. Robinson, S. M.), (Academic Press, 1980) 93–138.Google Scholar
[44]Kojima, M. and Hirabayashi, R., “Continuous deformations of nonlinear programs”, Mathematical Programming Study 21 (1984) 150–198.Google Scholar
[45]Krabs, W. and Weber, G.-W., personal communication, Darmstadt, Germany, 1994.Google Scholar
[46]Lempio, F. and Maurer, H., “Differential stability in optimal control problems”, Appl. Math. Optim. 5 (1979) 283–295.Google Scholar
[47]Malanowski, K., remark, Güstrow, Germany, 1991.Google Scholar
[48]Malanowski, K., “Regularity of solutions in stability analysis of optimization and optimal control problems”, Control and Cybernetics 23 (1994) 61–86.Google Scholar
[49]Mangasarian, O. L. and Fromovitz, S., “The Fritz John necessary optimality condition in the presence of equality and inequality constraints”, J. Math. Anal. Appl. 17 (1967) 37–47.Google Scholar
[50]Maurer, H., “Numerical solution of singular control problems using multiple shooting”, J. Optimization Theory and Applications 18 (1976) 235–257.CrossRefGoogle Scholar
[51]Maurer, H., “On optimal control problems with bounded state variables and control appearing linearly”, SIAM J. Control and Optimization 15 (1977) 345–362.CrossRefGoogle Scholar
[52]Maurer, H., “Differential stability in infinite-dimensional nonlinear programming”, Appl. Math. Optim. 6 (1980) 139–152.Google Scholar
[53]Maurer, H. and Pesch, H.-J., “Solution differentiability for parametric nonlinear control problems with control-state constraints”, Control and Cybernetics 23 (1994) 201–227.Google Scholar
[54]Maurer, H. and Pickenhain, S., “Second-order sufficient conditions for control problems with mixed control-state constraints”, preprint. University of Münster, Germany (1993).Google Scholar
[55]Milnor, J., “Morse theory”, Annals of Mathematical Studies 51 (Princeton University Press, 1963).Google Scholar
[56]Pontryagin, L. S., Boltryanski, V. G., Gamkrelidze, R. V. and Mishchenko, E. F., The Mathematical Theory of Optimal Processes (Interscience Publishers, J. Wiley, 1962).Google Scholar
[57]Rupp, Th., “Kontinuitätsmethoden zur Lösung einparametrischer semi-infiniter Optimierungsprob- leme”, thesis, University of Trier, 1988.Google Scholar
[58]Smale, S., “Algorithms for solving equations”, in Proc. Int. Congr. Math. I (ed. Gleason, M. S.), (AMS, Berkeley, 1986) 172–195.Google Scholar
[59]Smale, S., “Complexity of Bezout' theorem I. Geometric aspects”, Journal of the America Mathematical Society 6 (1993) 459–501.Google Scholar
[60]Smale, S., “Complexity of Bezout's theorem IV. Probability of success; extensions”, SIAM J. Numerical Analysis, to appear.Google Scholar
[61]Spanier, E. H., Algebraic Topology (McGraw-Hill, 1966).Google Scholar
[62]Thorn, R., Stabilité Structurelle et Morphogénèse: Essai d'une Théorie Générate des Modéles (W. A. Benjamin, Reading, MA, 1972).Google Scholar
[63]Walter, Th. and Weber, G.-W., personal communication, Darmstadt, 1994.Google Scholar
[64]Weber, G.-W., Charakterisierung struktureller Stabilität in der nichtlinearen Optimierung, thesis, Technical University of Aachen, Aachener Beiträge zur Mathematik 5, Augus-tinus-Buchhandlung, Aachen, Germany, 1992.Google Scholar
[65]Weber, G.-W., “Minimization of a max-type function: characterization of structural stability”, in Parametric Optimization and Related Topics III (eds. Guddat, J., Jongen, H.Th., Kummer, B. and Nožička, F.), (Peter Lang Verlag, Frankfurt a.M., Bern, New York, 1993) 519–538.Google Scholar
[66]Weber, G.-W., “Optimal control theory: on the global structure and connections with optimization. Parts 1,2”, preprints, Darmstadt University of Technology, Darmstadt, Germany, 1995.Google Scholar
[67]Wetterling, W. W. E., “Definitheitsbedingungen für relative Extrema bei Optimierungs- und Approximationsaufgaben”, Numer. Math. 15 (1970) 122–136.Google Scholar
[68]Yomdin, Y., “On the local structure of a generic central set”, Compositio Mathematica (1981) 225–238.Google Scholar
[69]Yomdin, Y, “Metric semialgebraic geometry with applications in smooth analysis”, preprint, Weizman Institute of Science, Rehovot, Israel (1988).Google Scholar
[70]Yomdin, Y, “Sard's theorem and its improved versions in numerical analysis”, preprint, Weizman Institute of Science, Rehovot, Israel (1988).Google Scholar
[71]Zolezzi, T., “Well posedness criteria in optimization with application to the calculus of variations”, Nonlinear Analysis - Theory, Methods, Applications, to appear.Google Scholar