Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dehghan, Mehdi
2002.
Numerical techniques for a parabolic equation subject to an overspecified boundary condition.
Applied Mathematics and Computation,
Vol. 132,
Issue. 2-3,
p.
299.
Dehghan, Mehdi
2003.
Parallel techniques for a boundary value problem with non-classic boundary conditions.
Applied Mathematics and Computation,
Vol. 137,
Issue. 2-3,
p.
399.
Dehghan, Mehdi
2003.
Numerical solution of a parabolic equation with non-local boundary specifications.
Applied Mathematics and Computation,
Vol. 145,
Issue. 1,
p.
185.
Dehghan, Mehdi
2004.
Numerical solution of a parabolic equation subject to specification of energy.
Applied Mathematics and Computation,
Vol. 149,
Issue. 1,
p.
31.
Dehghan, Mehdi
2004.
Application of the Adomian decomposition method for two-dimensional parabolic equation subject to nonstandard boundary specifications.
Applied Mathematics and Computation,
Vol. 157,
Issue. 2,
p.
549.
Dehghan, Mehdi
2005.
On the solution of an initial‐boundary value problem that combines Neumann and integral condition for the wave equation.
Numerical Methods for Partial Differential Equations,
Vol. 21,
Issue. 1,
p.
24.
Dehghan, Mehdi
2005.
Efficient techniques for the second-order parabolic equation subject to nonlocal specifications.
Applied Numerical Mathematics,
Vol. 52,
Issue. 1,
p.
39.
Dehghan, Mehdi
2006.
A computational study of the one‐dimensional parabolic equation subject to nonclassical boundary specifications.
Numerical Methods for Partial Differential Equations,
Vol. 22,
Issue. 1,
p.
220.
Dehghan, Mehdi
2007.
The one-dimensional heat equation subject to a boundary integral specification.
Chaos, Solitons & Fractals,
Vol. 32,
Issue. 2,
p.
661.
Soltanalizadeh, B.
2011.
Numerical analysis of the one-dimensional heat equation subject to a boundary integral specification.
Optics Communications,
Vol. 284,
Issue. 8,
p.
2109.
Yousefi, S.A.
Behroozifar, M.
and
Dehghan, Mehdi
2011.
The operational matrices of Bernstein polynomials for solving the parabolic equation subject to specification of the mass.
Journal of Computational and Applied Mathematics,
Vol. 235,
Issue. 17,
p.
5272.
Yousefi, S.A.
Barikbin, Zahra
and
Dehghan, Mehdi
2012.
Ritz‐Galerkin method with Bernstein polynomial basis for finding the product solution form of heat equation with non‐classic boundary conditions.
International Journal of Numerical Methods for Heat & Fluid Flow,
Vol. 22,
Issue. 1,
p.
39.
Tohidi, Emran
and
Toutounian, Faezeh
2016.
Numerical solution of time-dependent diffusion equations with nonlocal boundary conditions via a fast matrix approach.
Journal of the Egyptian Mathematical Society,
Vol. 24,
Issue. 1,
p.
86.
Barikbin, Z.
and
Keshavarz Hedayati, E.
2017.
Exact and approximation product solutions form of heat equation with nonlocal boundary conditions using Ritz–Galerkin method with Bernoulli polynomials basis.
Numerical Methods for Partial Differential Equations,
Vol. 33,
Issue. 4,
p.
1143.
Furati, Khaled M.
Mustapha, Kassem
Sarumi, Ibrahim O.
and
Iyiola, Olaniyi S.
2021.
Inverse source in two-parameter anomalous diffusion, numerical algorithms, and simulations over graded time meshes.
Computational and Applied Mathematics,
Vol. 40,
Issue. 1,
HAMMOUCH, Zakia
ZAHRA, Anam
REHMAN, Azız
and
MARDAN, Syed Ali
2022.
AN EFFICIENT NUMERICAL TECHNIQUE FOR SOLVING HEAT EQUATION WITH NONLOCAL BOUNDARY CONDITIONS.
Advances in the Theory of Nonlinear Analysis and its Application,
Vol. 6,
Issue. 2,
p.
157.


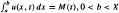 .
.