No CrossRef data available.
Article contents
ON MULTI-ASSET SPREAD OPTION PRICING IN A WICK–ITÔ–SKOROHOD INTEGRAL FRAMEWORK
Published online by Cambridge University Press: 24 May 2017
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We provide an elementary method for exploring pricing problems of one spread options within a fractional Wick–Itô–Skorohod integral framework. Its underlying assets come from two different interactive markets that are modelled by two mixed fractional Black–Scholes models with Hurst parameters,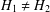 
$H_{1}\neq H_{2}$, where 
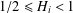$1/2\leq H_{i}<1$ for 
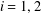$i=1,2$. Pricing formulae of these options with respect to strike price 
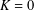$K=0$ or 
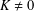$K\neq 0$ are given, and their application to the real market is examined.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2017 Australian Mathematical Society
References
Biagini, F., Hu, Y., Øksendal, B. and Zhang, T., Stochastic calculus for fractional Brownian motion and applications (Springer, London, 2008).CrossRefGoogle Scholar
Bianchi, S., Pantanella, A. and Pianese, A., “Modeling stock prices by multifractional Brownian motion: an improved estimation of the pointwise regularity”, Quant. Finance
11 (2011) 1–14; doi:10.1080/14697688.2011.594080.Google Scholar
Caldana, R. and Fusai, G., “A general closed-form spread option pricing formula”, J. Banking Finance
37 (2013) 4893–4906; http://dx.doi.org/10.1016/j.jbankfin.2013.08.016.Google Scholar
Carmona, R. and Durrleman, V., “Pricing and hedging spread options”, SIAM Rev.
45 (2003) 627–685; http://dx.doi.org/10.1137/S0036144503424798.CrossRefGoogle Scholar
Carr, P. and Madan, D., “Option valuation using the fast Fourier transform”, J. Comput. Finance
2 (1999) 61–73; http://dx.doi.org/10.21314/JCF.1999.043.Google Scholar
Dempster, M. and Hong, S., “Spread option valuation and the fast Fourier transform”, Math. Finance Bachelier Congr.
1 (2000) 203–220; http://dx.doi.org/10.1007/978-3-662-12429-1-10.Google Scholar
Deng, S., Li, M. and Zhou, J., “Closed-form approximations for spread option prices and Greeks”, J. Derivatives
16 (2008) 58–80.Google Scholar
Elliott, R. J. and Van der Hoek, J., “A general fractional white noise theory and applications to finance”, Math. Finance
13 (2003) 301–330; http://dx.doi.org/10.1111/1467-9965.00018.CrossRefGoogle Scholar
Fama, E. F., “The behaviour of stock market prices”, J. Bus.
38 (1965) 34–105; http://www.e-m-h.org/Fama65.pdf.Google Scholar
Hu, Y. and Øksendal, B., “Fractional white noise calculus and applications to finance”, Infin. Dimens. Anal. Quantum Probab. Relat. Top.
6 (2003) 1–32; http://dx.doi.org/10.1142/S0219025703001110.Google Scholar
Hurd, T. R. and Zhou, Z., “A Fourier transform method for spread option pricing”, SIAM J. Financial Math.
1 (2010) 142–157; http://dx.doi.org/10.1137/090750421.Google Scholar
Li, M., Zhou, J. and Deng, S. J., “Multi-asset spread option pricing and hedging”, Quant. Finance
10 (2010) 305–324; http://dx.doi.org/10.1080/14697680802626323.Google Scholar
Lo, A. W. and MacKinley, A. C., “Stock market prices do not follow random walks: Evidence from a simple specification test”, Rev Financ Stud.
1 (1988) 41–66; http://dx.doi.org/10.1093/rfs/1.1.41.Google Scholar
Necula, C., “Option pricing in a fractional Brownian motion environment”, SSRN Electronic J.
6 (2002) 258–273 ; http://dx.doi.org/10.2139/ssrn.1286833.Google Scholar
Peters, E., Fractal market analysis applying chaos theory to investment and economics (John Wiley & Sons Inc., Berlin, 2002).Google Scholar
Shimko, D., “Options on futures spreads: hedging, speculation and valuation”, J. Futures Mark.
14 (1994) 183–213; http://dx.doi.org/10.1002/fut.3990140206.CrossRefGoogle Scholar
Tao, X.-X. and Shi, Y.-F., “Option pricing on fractional correlated stocks”, Manag. Eng. Appl.
2010 (2010) 539–545.Google Scholar
You have
Access