Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T10:47:12.897Z Has data issue: false hasContentIssue false
  • English
  • Français

On a periodically forced, weakly damped pendulum. Part 3: Vertical forcing

Published online by Cambridge University Press:  17 February 2009

Peter J. Bryant  and
John W. Miles
Peter J. Bryant
Affiliation:
Department of Mathematics, University of Canterbury, Christchurch, New Zealand.
John W. Miles
Affiliation:
Institute of Geophysics and Planetary Physics, University of California at San Diego, La Jolla, California 92093, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the phase-locked solutions of the differential equation governing planar motion of a weakly damped pendulum forced by a prescribed, vertical acceleration εg sin ωt of its pivot, where ω and t are dimensionless, and the unit of time is the reciprocal of the natural frequency. Resonance curves and stability boundaries are presented for downward and inverted oscillations of periods T, 2T, 4T, …, where T (≡ 2π/ω) is the forcing period. Stable, downward oscillations are found to occur in distinct regions of the (ω, ε) plane, reminiscent of the regions of stability of the Mathieu equation (which describes the equivalent undamped, parametrically excited pendulum motion). 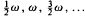The regions are dominated by oscillations of frequencies , each region being bounded on one side by a vertical state at rest in stable equilibrium and on the other side by a symmetry-breaking, period-doubling sequence to chaotic motion. Stable, inverted oscillations are found to occur also in distinct regions of the (ω, ε) plane, the principal oscillation in each region being symmetric with period 2T.

Type
Research Article
Information
The ANZIAM Journal , Volume 32 , Issue 1 , July 1990 , pp. 42 - 60
Copyright
Copyright © Australian Mathematical Society 1990

References

[1] Abramowitz, M. and Stegun, I. A. (eds.), Handbook of Mathematical Functions (Dover, New York, 1970), 722ff.Google Scholar
[2] Bryant, Peter J. and Miles, John W., “On a periodically forced, weakly damped pendulum. Part 1: Applied torque”, J. Austral. Math. Soc. Ser. B. 32 (1990) 1–22.Google Scholar
[3] Bryant, Peter J. and Miles, John W., “On a periodically forced, weakly damped pendulum. Part 2: Horizontal forcint”, J. Austral. Math. Soc. Ser. B. 32 (1990) 23–41.CrossRefGoogle Scholar
[4] Drazin, P. G. and Reid, W. H., Hydrodynamic Stability (Cambridge University Press, 1981), 357.Google Scholar
[5] Gollub, J. P. and Meyer, Christopher W., “Symmetry-breaking instabilities on a fluid surface”, Physica D 6 (1983) 337–346.Google Scholar
[6] Leven, R. W. and Koch, B. P., “Chaotic behaviour of a parametrically excited damped pendulum”, Phys. Lett. A 86 (1981) 71–74.Google Scholar
[7] Leven, R. W., Pompe, B., Wilke, C. and Koch, B. P., “Experiments on periodic and chaotic motions of a parametrically forced pendulum”, Physica D 16 (1985) 371–384.Google Scholar
[8] McLaughlin, J. B., “Period-doubling bifurcations and chaotic motion of a parametrically forced pendulum”, J. Stat. Phys. 24 (1981) 375.Google Scholar
[9] Miles, John W., “Nonlinear Faraday resonance”, J. Fluid Mech. 146 (1984) 285–302.Google Scholar
[10] Miles, John W., “Resonance and symmetry breaking for the pendulum”, Physica D 31 (1988) 252–268.Google Scholar