Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-25T09:06:31.250Z Has data issue: false hasContentIssue false
  • English
  • Français

OBLIQUE WAVE SCATTERING BY A RECTANGULAR SUBMARINE TRENCH

Part of: Incompressible inviscid fluids

Published online by Cambridge University Press:  16 March 2015

RUMPA CHAKRABORTY  and
B. N. MANDAL
RUMPA CHAKRABORTY*
Affiliation:
Physics and Applied Mathematics Unit, Indian Statistical Institute 203, B. T. Road, Kolkata 700108, India email [email protected], [email protected]
B. N. MANDAL
Affiliation:
Physics and Applied Mathematics Unit, Indian Statistical Institute 203, B. T. Road, Kolkata 700108, India email [email protected], [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

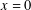The problem of oblique wave scattering by a rectangular submarine trench is investigated assuming a linearized theory of water waves. Due to the geometrical symmetry of the rectangular trench about the central line $x=0$, the boundary value problem is split into two separate problems involving the symmetric and antisymmetric potential functions. A multi-term Galerkin approximation involving ultra-spherical Gegenbauer polynomials is employed to solve the first-kind integral equations arising in the mathematical analysis of the problem. The reflection and transmission coefficients are computed numerically for various values of different parameters and different angles of incidence of the wave train. The coefficients are depicted graphically against the wave number for different situations. Some curves for these coefficients available in the literature and obtained by different methods are recovered.

Keywords

water wave scatteringrectangular submarine trenchoblique incident wavemulti-term Galerkin approximationreflection and transmission coefficients

MSC classification

Primary: 76B15: Water waves, gravity waves; dispersion and scattering, nonlinear interaction
Type
Research Article
Information
The ANZIAM Journal , Volume 56 , Issue 3 , January 2015 , pp. 286 - 298
Copyright
© 2015 Australian Mathematical Society 

References

Banerjea, S., Kanoria, M., Dolai, D. P. and Mandal, B. N., “Oblique wave scattering by a submerged thin wall with gap in finite depth water”, Appl. Ocean Res. 18 (1996) 319–327; doi:10.1016/S0141-1187(97)00002-3.Google Scholar
Das, P., Dolai, D. P. and Mandal, B. N., “Oblique wave diffraction by two parallel thin barriers with gaps”, J. Waterway Port Coast. Ocean Engrg. 123 (1997) 163–171; doi:10.1061/(ASCE)0733-950X(1997)123:4(163).CrossRefGoogle Scholar
Evans, D. V. and Fernyhough, M., “Edge waves along periodic coastlines. Part 2”, J. Fluid Mech. 297 (1995) 307–325; doi:10.1017/S0022112095003119.Google Scholar
Kanoria, M., “Water wave scattering by thick rectangular slotted barrier”, Appl. Ocean Res. 23 (2001) 285–298; doi:10.1016/S0141-1187(01)00018-9.Google Scholar
Kanoria, M., Dolai, D. P. and Mandal, B. N., “Water wave scattering by thick vertical barriers”, J. Engrg. Math. 35 (1999) 361–384; doi:10.1023/A:1004392622976.CrossRefGoogle Scholar
Kirby, J. T. and Dalrymple, R. A., “Propagation of obliquely incident water waves over a trench”, J. Fluid Mech. 133 (1983) 47–63; doi:10.1017/S0022112083001780.CrossRefGoogle Scholar
Kreisel, H., “Surface waves”, Quart. Appl. Math. 7 (1949) 21–44.Google Scholar
Lassiter, J. B., “The propagation of water waves over sediment pockets”, Ph. D. Thesis, Massachusetts Institute of Technology, 1972, http://hdl.handle.net/1721.1/13809.Google Scholar
Lee, J. J. and Ayer, R. M., “Wave propagation over a rectangular trench”, J. Fluid Mech. 110 (1981) 335–347; doi:10.1017/S0022112081000773.Google Scholar
Miles, J. W., “On surface wave diffraction by a trench”, J. Fluid Mech. 115 (1982) 315–325; doi:10.1017/S0022112082000779.Google Scholar
Porter, R. and Evans, D. V., “Complementary approximations to wave scattering by vertical barriers”, J. Fluid Mech. 294 (1995) 155–180; doi:10.1017/S0022112095002849.Google Scholar
Ursell, F., “The effect of a fixed vertical barrier on surface waves in deep water”, Proc. Cambridge Philos. Soc. 43 (1947) 374–382; doi:10.1017/S0305004100023604.CrossRefGoogle Scholar