Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T11:11:22.281Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON THE AXISYMMETRIC DIFFUSION EQUATION

Part of: Representations of solutions Miscellaneous topics - Partial differential equations Partial differential equations

Published online by Cambridge University Press:  21 July 2021

ALEXANDER E. PATKOWSKI Open the ORCID record for ALEXANDER E. PATKOWSKI [Opens in a new window]
ALEXANDER E. PATKOWSKI*
Affiliation:
1390 Bumps River Road, Centerville, MA02632, USA; e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the explicit solution to the axisymmetric diffusion equation. We recast the solution in the form of a Mellin inversion formula, and outline a method to compute a formula for 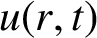$u(r,t)$ as a series using the Cauchy residue theorem. As a consequence, we are able to represent the solution to the axisymmetric diffusion equation as a rapidly converging series.

Keywords

axisymmetric diffusion equationBessel functionsMellin transforms

MSC classification

Primary: 35R10: Partial functional-differential equations
Secondary: 35B40: Asymptotic behavior of solutions 35C10: Series solutions
Type
Research Article
Information
The ANZIAM Journal , Volume 63 , Issue 3 , July 2021 , pp. 333 - 341
Check for updates
Copyright
© Australian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. and Stegun, I. A. (eds), “Confluent hypergeometric functions”, in: Handbook of mathematical functions with formulas, graphs, and mathematical tables, 9th printing (Dover, New York, 1972) Chapter 13, 503–515.Google Scholar
Boyadjiev, L. and Luchko, Yu., “Mellin integral transform approach to analyze the multidimensional diffusion-wave equations”, Chaos Solitons Fractals 102 (2017) 127–134; doi:10.1016/j.chaos.2017.03.050.CrossRefGoogle Scholar
Debnath, L., Nonlinear partial differential equations for scientists and engineers (Birkhauser, Boston, MA, 1997); doi:10.1007/978-0-8176-8265-1.CrossRefGoogle Scholar
Gradshteyn, I. S. and Ryzhik, I. M., Tables of integrals, series, and products, 7th edn (eds Jeffrey, A. and Zwillinger, D.), (Academic Press, New York, 2007); ISBN: 9780123736376.Google Scholar
Olver, F. W. J., Asymptotics and special functions (Academic Press, New York, 1974); doi:10.1016/C2013-0-11255-X.Google Scholar
Paris, R. B. and Kaminski, D., Asymptotics and Mellin–Barnes integrals (Cambridge University Press, Cambridge, 2001); doi:10.1017/CBO9780511546662.CrossRefGoogle Scholar
Szegö, G., Orthogonal polynomials, Volume 23 of Colloq. Publ. (American Mathematical Society, Providence, RI, 1939); doi:10.1090/coll/023.Google Scholar
Titchmarsh, E. C., Introduction to the theory of Fourier integrals, 2nd edn (Clarendon Press, Oxford, 1959).Google Scholar