Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-22T07:13:02.068Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on nondifferentiable symmetric duality

Published online by Cambridge University Press:  17 February 2009

B. D. Craven
B. D. Craven
Affiliation:
Mathematics Department, Univerisity of Melbourne, Parkville, Victoria 3052
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Under suitable hypotheses on the function f, the two constrained minimization problems:

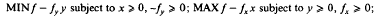
are well known each to be dual to the other. This symmetric duality result is now extended to a class of nonsmooth problems, assuming some convexity hypotheses. The first problem is generalized to:

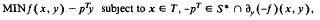
in which T and S are convex cones, S* is the dual cone of S, and ∂y denotes the subdifferential with respect to y. The usual method of proof uses second derivatives, which are no longer available. Therefore a different method is used, where a nonsmooth problem is approximated by a sequence of smooth problems. This duality result confirms a conjecture by Chandra, which had previously been proved only in special cases.

Type
Research Article
Information
The ANZIAM Journal , Volume 28 , Issue 1 , July 1986 , pp. 30 - 35
Copyright
Copyright © Australian Mathematical Society 1986

References

[1]Chandra, S., Craven, B. D. and Mond, B., “Symmetric dual fractional programming,” Z. Oper. Res. Ser. Theory, 29 (1985), 59–64.Google Scholar
[2]Clarke, F. H., “A new approach to Lagrange multipliers,” Math. Oper. Res. 1 (1976), 165–174.CrossRefGoogle Scholar
[3]Craven, B. D., Mathematical programming and control theory, (Chapman and Hall, London, 1978).CrossRefGoogle Scholar
[4]Craven, B. D., “Nondifferentiable optimization by smooth approximation,” Melbourne University, Mathematics Research Report 32 (1984), to appear in Optimization (1986).Google Scholar
[5]Craven, B. D. and Mond, B., “Transposition theorems for cone-convex functions,” SIAM J. Appl. Math. 24 (1973), 603–612.CrossRefGoogle Scholar