Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T11:02:00.362Z Has data issue: false hasContentIssue false
  • English
  • Français

A nonlinear difference equation with two parameters

Published online by Cambridge University Press:  17 February 2009

A. Brown
A. Brown
Affiliation:
Department of Theretical Physice, Research School of Physical Sciences, Australian National University, G.P.O. Box 4, Canberra, A. C. T. 2601.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The paper is mainly concerned with the difference equation

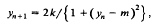
where k and m are parameters, with k > 0. This equation arises from a method proposed for solving a cubic equation by iteration and represents a standardised form of the general problem. In using the above equation it is essential to know when the iteration process converges and this is discussed by means of the usual stability criterion. Critical values are obtained for the occurrence of solutions with period two and period three and the stability of these solutions is also examined. This was done by considering the changes as k increases, for a give value of m, which makes it effectively a one-parameter problem, and it turns out that the change with k can differ strongly from the usual behaviour for a one-parameter difference equation. For m = 2, for example it appears that the usual picture of stable 2-cycle solutions giving way to stable 4-cycle solutions is valid for smaller values of k but the situation is recersed for larger values of k where stable 4-cycle solutions precede stable 2-cycle solutions. Similar anomalies arise for the 3-cycle solutions.

Type
Research Article
Information
The ANZIAM Journal , Volume 26 , Issue 4 , April 1985 , pp. 430 - 451
Copyright
Copyright © Australian Mathematical Society 1985

References

[1]Collet, P. and Eckmann, J. P., Iterated maps on the interval as dynamical systems (Birkhäuser, Boston, 1980).Google Scholar
[2]Coppel, W. A., “The solution of cubic equations by iteration”, Z. Angew. Math. Phys. 9a (1958), 380–383.CrossRefGoogle Scholar
[3]Coppel, W. A., private communication.Google Scholar
[4]Fletcher, A., Miller, J. C. P., Rosenhead, L. and Comrie, L. J., An index of mathematical tables (Blackwell Scientific Publications, Oxford, 2nd edition, 1962), Section 5.64.Google Scholar
[5]Frauenthal, J. C., Introduction to population modeling (Birkhäuser, Boston, 1980).Google Scholar
[6]Hartree, D. R., Numerical analysis (Clarendon Press, Oxford, 1952), 200.Google Scholar
[7]Hildebrand, F. B., Introduction to numerical analysis (McGraw-Hill, New York, 1956), 454–458.Google Scholar
[8]Lin, S. N., “A method of successive approximations of evaluating the real and complex roots of cubic and higher-order equations”, J. Math. Phys. 20 (1941), 231–242.CrossRefGoogle Scholar
[9]Lin, S. N., “A method for finding roots of algebraic equations”, J. Math. Phys. 22 (1943), 60–77.CrossRefGoogle Scholar
[10]May, R. M., “Simple mathematical models with very complicated dynamics”, Nature 261 (1976), 459–467.CrossRefGoogle ScholarPubMed
[11]Salzer, H. E., Richards, C. H. and Arsham, I., Table for the solution of cubic equations (McGraw-Hill, New York, 1958).Google Scholar