Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-22T07:13:24.987Z Has data issue: false hasContentIssue false
  • English
  • Français

A non-linear difference equation with two parameters. II

Published online by Cambridge University Press:  17 February 2009

A. Brown
A. Brown
Affiliation:
Department of Theoretical Physics, Research School of Physical Science, Australian National University, G.P.O. Box 4, Canberra, A.C.T. 2601.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The paper discusses solutions of period 4 for the difference equation

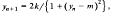
where k and m are real parameters, with k > 0. For given values of k and m there are at most three solutions with period 4 and equations are set up to determine the elements of these solutions and the stability of each solution. Only real solutions are considered. The procedure that is used to find these solutions allows unstable solutions to be identified as well as stable solutions.

In a previous paper, solutions of period 2 and period 3 were examined for this equation and there was evidence of anomalous behaviour in the way the stability intervals occurred. Some preliminary information about solutions of period 4 was mentioned in the discussion. The present paper provides more complete results, which confirm the anomalous behaviour and give a better idea of how the stability criterion changes for different families of solutions. These results are used to indicate the variety of behaviour that can be found for one-parameter systems by imposing suitable conditions on m and k.

Type
Research Article
Information
The ANZIAM Journal , Volume 27 , Issue 2 , October 1985 , pp. 145 - 166
Copyright
Copyright © Australian Mathematical Society 1985

References

[1]Bier, M. and Bountis, T. C., “Remerging trees in dynamical systems’, Phys. Letters 104A (1984), 239–244.CrossRefGoogle Scholar
[2]Brown, A., “A nonlinear difference equation with two parameters’, J. Austral. Math. Soc. Ser. B 26 (1985), 430–451.CrossRefGoogle Scholar
[3]Collet, P. and Eckmann, J. P., Iterated maps on the interval as dynamical systems (Birkhäuser, Boston, Mass., 1980).Google Scholar
[4]Coppel, W. A., “The solution of cubic equations by iteration”, Z. Angew. Math. Phys. 9a (1958), 380–383.CrossRefGoogle Scholar
[5]Holmes, P. J., “Bifurcation sequences in horseshoe maps: infinitely many routes to chaos’, Phys. Letters 104A (1984), 299–302.CrossRefGoogle Scholar
[6]Oppo, G. L. and Politi, A., “Collisions of Feigenbaum cascades’, Phys. Rev. 30A (1984), 435–441.CrossRefGoogle Scholar