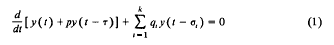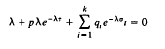Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Grove, E.A
Kulenović, M.R.S
and
Ladas, G
1987.
Sufficient conditions for oscillation and nonoscillation of neutral equations.
Journal of Differential Equations,
Vol. 68,
Issue. 3,
p.
373.
Schultz, S. W.
1988.
Necessary and sufficient conditions for the oscillations of bounded solutions.
Applicable Analysis,
Vol. 30,
Issue. 1-3,
p.
47.
Grammatikopoulos, M.K
Sficas, Y.G
and
Stavroulakis, I.P
1988.
Necessary and sufficient conditions for oscillations of neutral equations with several coefficients.
Journal of Differential Equations,
Vol. 76,
Issue. 2,
p.
294.
Györi, István
1989.
Oscillations of retarded differential equations of the neutral and the mixed types.
Journal of Mathematical Analysis and Applications,
Vol. 141,
Issue. 1,
p.
1.
Farrell, K
1989.
Necessary and sufficient conditions for oscillation of neutral equations with real coefficients.
Journal of Mathematical Analysis and Applications,
Vol. 140,
Issue. 1,
p.
251.
Györi, I.
1989.
Oscillation and comparison results in neutral differential equations and their applications to the delay logistic equation.
Computers & Mathematics with Applications,
Vol. 18,
Issue. 10-11,
p.
893.
Ladas, G
Partheniadis, E.C
and
Sficas, Y.G
1989.
Necessary and sufficient conditions for oscillations of second-order neutral equations.
Journal of Mathematical Analysis and Applications,
Vol. 138,
Issue. 1,
p.
214.
Arino, O
and
Győri, I
1989.
Necessary and sufficient condition for oscillation of a neutral differential system with several delays.
Journal of Differential Equations,
Vol. 81,
Issue. 1,
p.
98.
Zhang, B.G
1989.
Oscillation of first order neutral functional differential equations.
Journal of Mathematical Analysis and Applications,
Vol. 139,
Issue. 2,
p.
311.
Stavroulakis, I. P.
1989.
Oscillations of mixed neutral equations.
Hiroshima Mathematical Journal,
Vol. 19,
Issue. 3,
Ladas, G.
and
Schults, S. W.
1989.
On oscillations of neutral equations with mixed arguments.
Hiroshima Mathematical Journal,
Vol. 19,
Issue. 2,
Grove, E. A.
Kulenovic, M. R. S.
and
Ladas, G.
1990.
A Myskis‐Type Comparison Result for Neutral Equations.
Mathematische Nachrichten,
Vol. 146,
Issue. 13-14,
p.
195.
Huang, Qing Guang
and
Chen, Shao Zhu
1990.
Oscillation of neutral differential equations with periodic coefficients.
Proceedings of the American Mathematical Society,
Vol. 110,
Issue. 4,
p.
997.
Gopalsamy, K
and
Zhang, B.G
1990.
Oscillation and nonoscillation in first order neutral differential equations.
Journal of Mathematical Analysis and Applications,
Vol. 151,
Issue. 1,
p.
42.
Yuanji, Cheng
1991.
Oscillation in Linear Differential Equations with Continuous Distribution of Time Lag.
Mathematische Nachrichten,
Vol. 153,
Issue. 1,
p.
217.
Gopalsamy, Kondalsamy
and
Lalli, Bikkar S.
1991.
Necessary and sufficient conditions for ``zero crossing'' in integrodifferential equations.
Tohoku Mathematical Journal,
Vol. 43,
Issue. 2,
Jaroš, Jaroslav
1991.
An oscillation test for a class of linear neutral differential equations.
Journal of Mathematical Analysis and Applications,
Vol. 159,
Issue. 2,
p.
406.
Lu, Wudu
1991.
Oscillations of high order neutral differential equations with oscillatory coefficient.
Acta Mathematicae Applicatae Sinica,
Vol. 7,
Issue. 2,
p.
135.
Marušiak, Pavol
1992.
Nonoscillatory solutions of systems of neutral differential equations.
Hiroshima Mathematical Journal,
Vol. 22,
Issue. 3,
Bilchev, S. J.
Grammatikopoulos, M. K.
and
Stavroulakis, I. P.
1992.
Oscillations of higher order neutral differential equations.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 52,
Issue. 2,
p.
261.