Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-25T10:15:34.252Z Has data issue: false hasContentIssue false
  • English
  • Français

n-Dimensional first integral and similarity solutions for two-phase flow

Published online by Cambridge University Press:  17 February 2009

S. W. Weeks ,
G. C. Sander  and
J.-Y. Parlange
S. W. Weeks
Affiliation:
School of Mathematical Sciences, Queensland University of Technology, GPO Box 2434, Brisbane QLD 4001, Australia; e-mail: [email protected].
G. C. Sander
Affiliation:
Department of Civil and Building Engineering, Loughborough University, Loughborough, LE11 3TU, England; e-mail: [email protected].
J.-Y. Parlange
Affiliation:
Department of Biological and Environmental Engineering, Riley-Robb Hall, Cornell University, Ithaca, N.Y., USA; e-mail: [email protected].
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper considers similarity solutions of the multi-dimensional transport equation for the unsteady flow of two viscous incompressible fluids. We show that in plane, cylindrical and spherical geometries, the flow equation can be reduced to a weakly-coupled system of two first-order nonlinear ordinary differential equations. This occurs when the two phase diffusivity D(θ) satisfies (D/D′)′ = 1/α and the fractional flow function f (θ) satisfies df/dθ = kDn/2, where n is a geometry index (1, 2 or 3), α and k are constants and primes denote differentiation with respect to the water content θ. Solutions are obtained for time dependent flux boundary conditions. Unlike single-phase flow, for two-phase flow with n = 2 or 3, a saturated zone around the injection point will only occur provided the two conditions 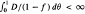and f′(1) ≠ 0 are satisfied. The latter condition is important due to the prevalence of functional forms of f (θ) in oil/water flow literature having the property f′(1) = 0.

Type
Research Article
Information
The ANZIAM Journal , Volume 44 , Issue 3 , January 2003 , pp. 365 - 380
Copyright
Copyright © Australian Mathematical Society 2003

References

[1]Allen, M. B. III, “Numerical modelling of multiphase flow in porous media”, Adv. Water Resour. 8 (1980) 163–186.Google Scholar
[2]Bluman, G. W. and Kumei, S., “On the remarkable nonlinear diffusion equation (∂/∂x)(a(u + b)−2(∂u/∂x)) – (∂u/∂t) = 0”, J. Math. Phys. 21 (1980) 1019–1023.CrossRefGoogle Scholar
[3]Bond, W. J. and Collis-George, N., “Ponded infiltration into simple soil systems: 1. The saturation and transition zones in the moisture content profile”, Soil Sci. Soc. Amer. J. 131 (1981) 202–209.CrossRefGoogle Scholar
[4]Celia, M. A. and Binning, P., “A mass conservative numerical solution for two-phase flow in porous media with application to unsaturated flow”, Water Resour Res. 28 (1992) 2819–282.CrossRefGoogle Scholar
[5]Chen, Z. X., “Some invariant solutions to two-phase displacement problems including capillary effect”, SPEJ 05 (1988) 691–700.Google Scholar
[6]Faust, C. R., Guswa, J. H. and Mercer, J. W., “Simulation of three-dimensional flow of immiscible fluids within and below the unsaturated zone”, Water Resour Res. 12 (1989) 2449–2464.Google Scholar
[7]Fokas, A. S. and Yortsos, Y. C., “On the exactly solvable equation S t = [(βS + γ)−2Sx]x + α(βS + γ)−2Sx, occurring in two-phase flow in porous media”, SIAM J. Appl. Math. 42 (1982) 318–332.CrossRefGoogle Scholar
[8]McWhorter, D. B., Infiltration affected by flow of air, Hydrology papers 49 (CSU, Fort Collins, Colorado, 1971).Google Scholar
[9]McWhorter, D. B. and Sunada, D. K., “Exact integral solutions for two-phase flow”, Water Resour. Res. 26 (1990) 399–413.CrossRefGoogle Scholar
[10]Parlange, J.-Y., “Theory of water movement in soils. One-dimensionalabsorption”, Soil Sci. 111 (1971) 134–137.CrossRefGoogle Scholar
[11]Parlange, J.-Y., “On solving the flow equation in unsaturated soils by optimization: horizontal infiltration”, Soil Sci. Soc. Amer. J. Proc. 39 (1975) 415–418.CrossRefGoogle Scholar
[12]Parlange, J.-Y. and Braddock, R. D., “A note on some similarity solutions of the diffusion equation”, J. Appl. Math. Phys. (ZAMP) 31 (1980) 653–656.Google Scholar
[13]Parlange, J.-Y., Braddock, R. D. and Chu, B. T., “First integrals of the diffusion equation; An extension of the Fujita solutions”, Soil Sci. Soc. Amer. J. 44 (1980) 908–911.CrossRefGoogle Scholar
[14]Parlange, J.-Y., Braddock, R. D., Sander, G. C. and Stagnitti, F., “Three-dimensional similarity solutions of the nonlinear diffusion equation from optimization and first integrals”, J. Austral. Math. Soc. Ser. B 23 (1982) 297–309.Google Scholar
[15]Parlange, J.-Y., Braddock, R. D. and Voss, G., “Two-dimensional similarity solutions of the nonlinear diffusion equation from optimization and first integrals”, Soil Sci. 131 (1981) 1–8.CrossRefGoogle Scholar
[16]Rogers, C., Stallybrass, M. P. and Clement, D. A.. “On two-phase infiltration under gravity and with boundary infiltration: Application of a Backlünd transformation”, Nonlinear Anal., Theory and Appl. 7 (1983) 785–799.Google Scholar
[17]Sander, G. C., Norbury, J. and Weeks, S. W., “An exact solution to the nonlinear diffusion-convection equation for two-phase flow”, Q. J. Mech. Appl. Math. 46 (1993) 709–727.CrossRefGoogle Scholar
[18]Sander, G. C., Parlange, J.-Y. and Hogarth, W. L., “Extension of the Fujita solution to air and water movement in soils”, Water Resour. Res. 24 (1988) 1187–1191.CrossRefGoogle Scholar
[19]Sander, G. C., Parlange, J.-Y., Hogarth, W. L. and Braddock, R. D., “Similarity and first integral solutions for air and water diffusion in soils and comparison with optimal results”, Soil Sci. 138 (1984) 321–325.Google Scholar
[20]Sleep, B. E. and Sykes, J. F., “Compositional simulation of groundwater contamination by organic compounds 2. Model applications”, Water Resour. Res. 29 (1993) 1709–1718.CrossRefGoogle Scholar
[21]Sposito, G., “Lie group invariance of the Richards equation”, in Dynamics of fluid in hierarchal porous media (ed. Cushman, J. H.), (Academic Press, London, 1990) 327–347.Google Scholar
[22]Sposito, G., “Recent advances associated with soil water in the unsaturated zone”, Rev. Geophys. Suppl. (1995) 1059–1065.Google Scholar
[23]Stothoff, S. A. and Pinder, G. F., “A boundary integral technique for multiple-front simulation of incompressible, immiscible flow in porous media”, Water Resour. Res. 28 (1992) 2067–2076.CrossRefGoogle Scholar
[24]Weeks, S. W., Sander, G. C., Lisle, I. G. and Parlange, J.-Y., “Similarity solutions of radially symmetric two-phase flow”. J. Appl. Math. Phys. (ZAMP) 45 (1994) 841–853.Google Scholar