No CrossRef data available.
Article contents
Multiple-term approximations for Appell's F1 function
Published online by Cambridge University Press: 17 February 2009
Abstract
In this paper computational issues of Appell's F1 function
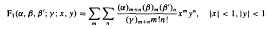
are addressed. A novel technique is used in the derivation of highly efficient multiple-term approximations of this function (including asymptotic ones). Simple structured single- and double-term approximations, as the first two candidates of this multiple-term representa-tion, are developed in closed form. Error analysis shows that- the developed algorithms are superior to existing approximations for the same number of terms. The formulation presented is highly efficient and could be extended to a wide class of special functions.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1997


