Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-25T09:15:50.606Z Has data issue: false hasContentIssue false
  • English
  • Français

MATRIX ANALYSES ON THE DAI–LIAO CONJUGATE GRADIENT METHOD

Part of: Numerical methods in calculus of variations and optimal control

Published online by Cambridge University Press:  09 May 2019

Z. AMINIFARD Open the ORCID record for Z. AMINIFARD [Opens in a new window]  and
S. BABAIE-KAFAKI Open the ORCID record for S. BABAIE-KAFAKI [Opens in a new window]
Z. AMINIFARD
Affiliation:
Department of Mathematics, Faculty of Mathematics, Statistics and Computer Science, Semnan University, PO Box 35195-363, Semnan, Iran email [email protected], [email protected]
S. BABAIE-KAFAKI*
Affiliation:
Department of Mathematics, Faculty of Mathematics, Statistics and Computer Science, Semnan University, PO Box 35195-363, Semnan, Iran email [email protected], [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Some optimal choices for a parameter of the Dai–Liao conjugate gradient method are proposed by conducting matrix analyses of the method. More precisely, first the 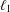$\ell _{1}$ and 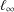$\ell _{\infty }$ norm condition numbers of the search direction matrix are minimized, yielding two adaptive choices for the Dai–Liao parameter. Then we show that a recent formula for computing this parameter which guarantees the descent property can be considered as a minimizer of the spectral condition number as well as the well-known measure function for a symmetrized version of the search direction matrix. Brief convergence analyses are also carried out. Finally, some numerical experiments on a set of test problems related to constrained and unconstrained testing environment, are conducted using a well-known performance profile.

Keywords

unconstrained optimizationconjugate gradient methodmatrix normDai–Liao parametercondition number

MSC classification

Primary: 90C53: Methods of quasi-Newton type
Secondary: 49M37: Methods of nonlinear programming type 65K05: Mathematical programming methods
Type
Research Article
Information
The ANZIAM Journal , Volume 61 , Issue 2 , April 2019 , pp. 195 - 203
Copyright
© 2019 Australian Mathematical Society 

References

Andrei, N., “Open problems in conjugate gradient algorithms for unconstrained optimization”, Bull. Malays. Math. Sci. Soc. 34 (2011) 319–330; http://emis.ams.org/journals/BMMSS/pdf/v34n2/v34n2p11.pdf.Google Scholar
Babaie-Kafaki, S. and Ghanbari, R., “The Dai–Liao nonlinear conjugate gradient method with optimal parameter choices”, European J. Oper. Res. 234 (2014) 625–630; doi:10.1016/j.ejor.2013.11.012.Google Scholar
Babaie-Kafaki, S. and Ghanbari, R., “A descent family of Dai–Liao conjugate gradient methods”, Optim. Methods Softw. 29 (2014) 583–591; doi:10.1080/10556788.2013.833199.Google Scholar
Babaie-Kafaki, S. and Ghanbari, R., “Two optimal Dai–Liao conjugate gradient methods”, Optimization 64 (2015) 2277–2287; doi:10.1080/02331934.2014.938072.Google Scholar
Babaie-Kafaki, S. and Ghanbari, R., “A class of adaptive Dai–Liao conjugate gradient methods based on the scaled memoryless BFGS update”, 4OR 15 (2017) 85–92; doi:10.1007/s10288-016-0323-1.Google Scholar
Byrd, R. H. and Nocedal, J., “A tool for the analysis of quasi-Newton methods with application to unconstrained minimization”, SIAM J. Numer. Anal. 26 (1989) 727–739; doi:10.1137/0726042.Google Scholar
Dai, Y. H., Han, J. Y., Liu, G. H., Sun, D. F., Yin, H. X. and Yuan, Y. X., “Convergence properties of nonlinear conjugate gradient methods”, SIAM J. Optim. 10 (1999) 348–358; doi:10.1137/S1052623494268443.Google Scholar
Dai, Y. H. and Kou, C. X., “A nonlinear conjugate gradient algorithm with an optimal property and an improved Wolfe line search”, SIAM J. Optim. 23 (2013) 296–320; doi:10.1137/100813026.Google Scholar
Dai, Y. H. and Liao, L. Z., “New conjugacy conditions and related nonlinear conjugate gradient methods”, Appl. Math. Optim. 43 (2001) 87–101; doi:10.1007/s002450010019.Google Scholar
Dolan, E. D. and Moré, J. J., “Benchmarking optimization software with performance profiles”, Math. Program. Ser. A 91(2) (2002) 201–213; doi:10.1007/s101070100263.Google Scholar
Fatemi, M., “An optimal parameter for Dai–Liao family of conjugate gradient methods”, J. Optim. Theory Appl. 169 (2016) 587–605; doi:10.1007/s10957-015-0786-9.Google Scholar
Gould, N. I. M., Orban, D. and Toint, P. L., “CUTEr: a constrained and unconstrained testing environment, revisited”, ACM Trans. Math. Software 29 (2003) 373–394; doi:10.1145/962437.962439.Google Scholar
Hager, W. W. and Zhang, H., “A new conjugate gradient method with guaranteed descent and an efficient line search”, SIAM J. Optim. 16 (2005) 170–192; doi:10.1137/030601880.Google Scholar
Hager, W. W. and Zhang, H., “Algorithm 851: CG-descent, a conjugate gradient method with guaranteed descent”, ACM Trans. Math. Software 32 (2006) 113–137; doi:10.1145/1132973.1132979.Google Scholar
Hager, W. W. and Zhang, H., “A survey of nonlinear conjugate gradient methods”, Pac. J. Optim. 2(1) (2006) 35–58; https://www.caam.rice.edu/∼yzhang/caam554/pdf/cgsurvey.pdf.Google Scholar
Hestenes, M. R. and Stiefel, E., “Methods of conjugate gradients for solving linear systems”, J. Res. Nat. Bur. Stand. 49 (1952) 409–436; doi:10.6028/jres.049.044.Google Scholar
Nocedal, J. and Wright, S. J., Numerical optimization, Springer Ser. Oper. Res. Financ. Eng. (Springer, New York, 2006); doi:10.1007/978-0-387-40065-5.Google Scholar
Powell, M. J. D., “Some global convergence properties of a variable metric algorithm for minimization without exact line searches”, in: Nonlinear programming, Volume 9 of SIAM–AMS Proc. (eds Cottle, R. W. and Lemke, C. E.), (American Mathematical Society, Providence, RI, 1976) 53–72.Google Scholar
Sun, W. and Yuan, Y. X., Optimization theory and methods: nonlinear programming (Springer, New York, 2006); https://www.springer.com/gp/book/9780387249759.Google Scholar
Watkins, D. S., Fundamentals of matrix computations (John Wiley, New York, 2002); https://www.wiley.com/enus/Fundamentals+of+Matrix+Computations%2C+3rd+Edition-p-9780470528334.Google Scholar
Xu, C. and Zhang, J. Z., “A survey of quasi-Newton equations and quasi-Newton methods for optimization”, Ann. Oper. Res. 103 (2001) 213–234; doi:10.1023/A:1012959223138.Google Scholar