Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T11:45:03.915Z Has data issue: false hasContentIssue false
  • English
  • Français

Inverse power law potentials about polygonal prisms and in polygonal cavities

Published online by Cambridge University Press:  17 February 2009

J. R. Philip
J. R. Philip
Affiliation:
CSIRO Division of Environmental Mechanics, P.O. Box 821, Canberra City, A.C.T. 2601, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The effects on adsorption of the geometry of the solid may be studied through calculations based on a (distance)−ε (ε> 3) intermolecular potential. This paper establishes the result that the potential due to an infinitely long polygonal homogeneous solid prism, at position r in the plane of its right section, is – 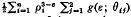. Here ρi = ∣ r − ri ∣, where the ri are the position vectors of the n vertices of the polygon, and θij are the angles r − ri makes with the two sides of the polygon which meet at vertex ri. The g's are exact functions of θij. They are, in general, integrals of associated Legendre functions, but they are elementary for ε an even integer. A similar result holds for the potential within an infinitely long polygonal prismatic cavity. The analysis involves a systematic superposition schema and the concept of a supplementary potential with datum within the solid at infinity. The cases ε = 6 and ε = 4 are treated in detail and illustrative solutions given for the following configurations: semi-infinite laminae, deep rectangular cracks, square prisms, square prismatic cavities and regular n-gonal prismatic cavities.

Type
Research Article
Information
The ANZIAM Journal , Volume 20 , Issue 2 , December 1977 , pp. 241 - 253
Copyright
Copyright © Australian Mathematical Society 1977

References

REFERENCES

[1]Clifford, J., “Properties of water in capillaries and thin films”, in Water, a comprehensive treatise (ed. Franks, F.) (Plenum, New York, 1975), Vol. 5, pp. 75–132.Google Scholar
[2]Erdélyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F. G., Higher transcendental functions (McGraw-Hill, New York, 1953), Vol. 1, p. 160, equation (33).Google Scholar
[3]Everett, D. H., “The effect of adsorption on the interaction between solid particles”, Pure and Appl. Chem. 48 (1976), 419–425.Google Scholar
[4]Forder, H. G., The foundations of Euclidean geometry (Dover, New York, 1958), pp. 244–254.Google Scholar
[5]MacMillan, W. D., The theory of the potential (Dover, New York, 1958), pp. 72–80.Google Scholar
[6]Philip, J. R., “Unitary approach to capillary condensation and adsorption”, J. Chem. Phys. 66 (1977), 5069–5075.Google Scholar
[7]Philip, J. R., “Adsorption and geometry: the boundary ayer approximation”, J. Chem. Phys. 67 (1977), 1732–1741.CrossRefGoogle Scholar
[8]Philip, J. R., “Inverse power law potentials in rectangular configurations”, Z. angew. Math. Phys. (in press).Google Scholar
[9]Sheludko, A., “Thin liquid films”, Adv. Coll. Interface Sci. 1 (1967), 390–464.CrossRefGoogle Scholar
[10]Steele, W. A. and Halsey, O. D. Jr, “The interaction of gas molecules with capillary and crystal lattice surfaces”, J. Phys. Chem. 59 (1955), 57–65.Google Scholar
[11]Waidvogel, J., “The Newtonian potential of a homogeneous cube”, Z. angew. Math. Phys. 27 (1976), 867–871.Google Scholar