Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T10:55:23.321Z Has data issue: false hasContentIssue false
  • English
  • Français

THE INFLUENCE OF INCREASING LIFE EXPECTANCY ON THE DYNAMICS OF SIRS SYSTEMS WITH IMMUNE BOOSTING

Published online by Cambridge University Press:  09 April 2013

M. P. DAFILIS ,
F. FRASCOLI ,
J. G. WOOD  and
J. M. MCCAW
M. P. DAFILIS*
Affiliation:
Melbourne School of Population Health and Global Health & Murdoch Childrens Research Institute, The University of Melbourne, Victoria 3010, Australia
F. FRASCOLI*
Affiliation:
Department of Mathematics and Statistics, The University of Melbourne, Victoria 3010, Australia
J. G. WOOD*
Affiliation:
School of Public Health and Community Medicine, The University of New South Wales, Sydney 2052, Australia
J. M. MCCAW*
Affiliation:
Melbourne School of Population Health and Global Health & Murdoch Childrens Research Institute, The University of Melbourne, Victoria 3010, Australia
*
✉[email protected]
✉[email protected]
✉[email protected]
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Endemic infectious diseases constantly circulate in human populations, with prevalence fluctuating about a (theoretical and unobserved) time-independent equilibrium. For diseases for which acquired immunity is not lifelong, the classic susceptible–infectious–recovered–susceptible (SIRS) model provides a framework within which to consider temporal trends in the observed epidemiology. However, in some cases (notably pertussis), sustained multiannual fluctuations are observed, whereas the SIRS model is characterized by damped oscillatory dynamics for all biologically meaningful choices of model parameters. We show that a model that allows for “boosting” of immunity may naturally give rise to undamped oscillatory behaviour for biologically realistic parameter choices. The life expectancy of the population is critical in determining the characteristic dynamics of the system. 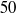For life expectancies up to approximately $50$ years, we find that, even with boosting, damped oscillatory dynamics persist. For increasing life expectancy, the system may sustain oscillatory dynamics, or even exhibit bistable behaviour, in which both stable point attractor and limit cycle dynamics may coexist. Our results suggest that rising life expectancy may induce changes in the characteristic dynamics of infections for which immunity is not lifelong, with potential implications for disease control strategies.

Keywords

infectious diseasemathematical modeldynamical systems

MSC classification

Secondary: 92D30: Epidemiology
Type
Research Article
Information
The ANZIAM Journal , Volume 54 , Issue 1-2 , October 2012 , pp. 50 - 63
Copyright
Copyright ©2013 Australian Mathematical Society 

References

Anderson, R. M and May, R. M., Infectious diseases of humans: dynamics and control (Oxford University Press, Oxford, 1992).Google Scholar
Bartlett, M. S., “Measles periodicity and community size”, J. R. Stat. Soc. A 120 (1957) 48–70; doi:10.2307/2342553.CrossRefGoogle Scholar
Bauch, C. T. and Earn, D. J. D., “Transients and attractors in epidemics”, Proc. R. Soc. Lond. B 270 (2003) 1573–1578; doi:10.1098/rspb.2003.2410.CrossRefGoogle ScholarPubMed
Van Damme, P. and Burgess, M., “Immunogenicity of a combined diphtheria–tetanus–acellular pertussis vaccine in adults”, Vaccine 22 (2004) 305–308; doi:10.1016/j.vaccine.2003.08.012.CrossRefGoogle ScholarPubMed
Doedel, E. J., “AUTO: a program for the automatic bifurcation analysis of autonomous systems”, Congr. Numer. 30 (1981) 265–284.Google Scholar
Doedel, E. J., AUTO-07P: Continuation and bifurcation software for ordinary differential equations, 2007; http://www.ma.hw.ac.uk/~gabriel/auto07/auto.html.Google Scholar
Doedel, E. J., Champneys, A. R., Fairgrieve, T. F., Kuznetsov, Y. A., Sandstede, B. and Wang, X., AUTO 97: Continuation and bifurcation software for ordinary differential equations (with HomCont), 1997.Google Scholar
Earn, D. J. D, Rohani, P., Bolker, B. M. and Grenfell, B. T., “A simple model for complex dynamical transitions in epidemics”, Science 287 (2000) 667–670; doi:10.1126/science.287.5453.667.CrossRefGoogle ScholarPubMed
Ermentrout, B., “Simulating, analyzing, and animating dynamical systems: a guide to XPPAUT for researchers and students”, Volume 14 of Software, Environments, and Tools (Society for Industrial and Applied Mathematics, Philadelphia, 2002).Google Scholar
Keeling, M. J. and Rohani, P., Modeling infectious diseases in humans and animals (Princeton University Press, Princeton, NJ, 2008).CrossRefGoogle Scholar
Lavine, J. S., King, A. A. and Bjørnstad, O. N., “Natural immune boosting in pertussis dynamics and the potential for long-term vaccine failure”, Proc. Natl. Acad. Sci. 108 (2011) 7259–7264; doi:10.1073/pnas.1014394108.CrossRefGoogle ScholarPubMed